Question

Two charged objects are separated by a distance $d$ as shown. The angle between the line joining the objects and the horizontal is $30^\circ $. Consider the (x,y) coordinate system with origin at the location of object 2. Calculate ${P_{21}}$the position vector of object 1 as measured from object 2. Express your answer in terms of $\hat i$, $\hat j$ and $d$ as needed.

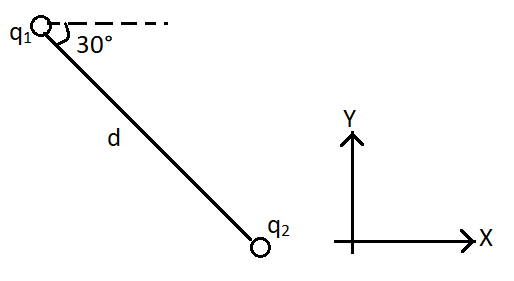
Answer 1

Hint: From the question it is given that the angle between the line joining the 2 objects and horizontal is $30^\circ $. So we can find the x component and the y component of the position vector of the object 1. Then using those values, we can find the position vector $\Rightarrow {P_{21}}$ in terms of $\hat i$, $\hat j$ and $d$.
Formula used: In this solution we will be using the following formula,
$\Rightarrow {P_{21}} = x\hat i + y\hat j$
where ${P_{21}}$ is the position vector
$x$ is the x component of position and $y$ is the y component of position.

Complete step by step solution:
In the problem it is given that the origin is considered in the position of the object 2. So we can break the position vector of the object 1 in the terms of the x and y components.
We can redraw the image as,

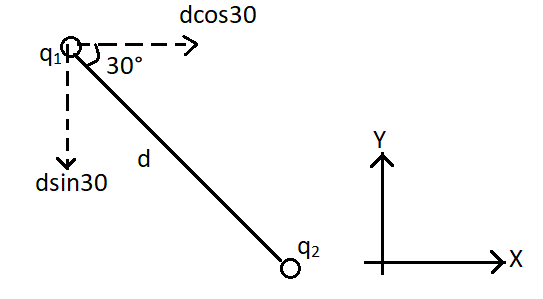
Now from the diagram, we can see that the horizontal component of the position vector is $d\cos 30^\circ $. This component coincides with the positive x axis and hence it is the x component. Therefore, $x = d\cos 30^\circ $. Again the vertical component of the position vector is $d\sin 30^\circ $. This component coincides with the negative y axis and hence it is the y component. Therefore, $y = d\sin 30^\circ $
Therefore, we can write the position vector as,
$\Rightarrow {P_{21}} = x\hat i + y\left( { - \hat j} \right)$
Substituting the values
$\Rightarrow {P_{21}} = d\cos 30\hat i + d\sin 30\left( { - \hat j} \right)$
Now the value of $\cos 30$is $\dfrac{{\sqrt 3 }}{2}$ and the value of $\sin 30$ is $\dfrac{1}{2}$
So substituting the values we get, ${P_{21}} = \dfrac{{\sqrt 3 }}{2}d\hat i - \dfrac{1}{2}d\hat j$
Now taking common we get,
$\Rightarrow {P_{21}} = \dfrac{d}{2}\left( {\sqrt 3 \hat i - \hat j} \right)$
This is the position vector of the object 1 with respect to the object 2.

Note:
In the solution we have taken the unit vector along the positive x axis as $\hat i$ and that along the positive y axis is $\hat j$. The y component of the position vector is directed towards the negative y axis. So we have used $\left( { - \hat j} \right)$ in the solution.