Question

Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.

Answer 1

Hint: Firstly, recall the expression for the electric field of a conducting sphere. Also, express the charge of the spheres in terms of capacitance and hence in terms of their radii. Now do necessary substitutions and thus get the ratio of electric fields on the conducting spheres. Also, give the explanation recalling that the charge density is directly proportional to the electric field.

Formula used:
Electric field on the surface of sphere,
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}}$
Charge,
$Q=CV$

Complete Step by step solution:
In the question, we are given two conducting spheres of radii a and b that are connected by a wire. We are asked to find the ratio of electric fields at the surfaces of the two spheres.

Also, using this result we are asked to explain why the sharper ends have higher charge density than the flatter portions.

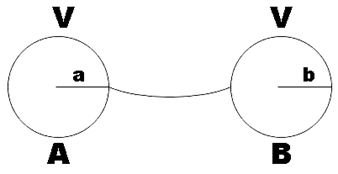
As the two spheres A and B are connected by a wire, their potentials will be the same. Let ${{Q}_{A}}$ and${{Q}_{B}}$ be the charges of the spheres and ${{C}_{A}}$ and ${{C}_{B}}$ their respective capacitances.

We know that electric field on a sphere of radius r is given by,
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}}$

Then the ratio of the electric fields at the surfaces of spheres A and B would be,
$\dfrac{{{E}_{A}}}{{{E}_{B}}}=\dfrac{\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}_{A}}}{{{a}^{2}}}}{\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{Q}_{B}}}{{{b}^{2}}}}$
$\therefore \dfrac{{{E}_{A}}}{{{E}_{B}}}=\dfrac{{{Q}_{A}}}{{{Q}_{B}}}\times \dfrac{{{b}^{2}}}{{{a}^{2}}}$ ………………………………………… (1)

Ratio of the charges of spheres A and B,
$\dfrac{{{Q}_{A}}}{{{Q}_{B}}}=\dfrac{{{C}_{A}}V}{{{C}_{B}}V}$

But, capacitance of a conducting sphere is proportional to its radius.
$\dfrac{{{C}_{A}}}{{{C}_{B}}}=\dfrac{a}{b}$
$\therefore \dfrac{{{Q}_{A}}}{{{Q}_{B}}}=\dfrac{a}{b}$ …………………………………………… (2)

Substituting (2) in (1) we get,
$\dfrac{{{E}_{A}}}{{{E}_{B}}}=\dfrac{a}{b}\times \dfrac{{{b}^{2}}}{{{a}^{2}}}$
$\therefore \dfrac{{{E}_{A}}}{{{E}_{B}}}=\dfrac{b}{a}$ ……………………………………………… (3)

Thereby, we have found the ratio of electric fields of the spheres.

We know that charge densities of the spheres are directly proportional to the electric fields, so,
$\dfrac{{{\sigma }_{A}}}{{{\sigma }_{B}}}=\dfrac{{{E}_{A}}}{{{E}_{B}}}$
Where, ${{\sigma }_{A}}$ and${{\sigma }_{B}}$ are the charge densities of spheres A and B respectively. Now, from (3) we get,
$\dfrac{{{\sigma }_{A}}}{{{\sigma }_{B}}}=\dfrac{b}{a}$

Hence, we found that the charge density of the conducting sphere is inversely proportional to its radius.

As the sharper ends have a smaller radius than that of the flatter portions, their charge density will definitely be higher than that of the latter.

Note:
For a sphere of symmetrical distribution of charge, the electric field outside the sphere is found to be similar to that from a point charge as per Gauss’s law. Also, in the case of conducting spheres, the electric field inside is found to be zero. Also, the potential of a conducting sphere of radius r is given by,
$V=\dfrac{kQ}{r}$