Question

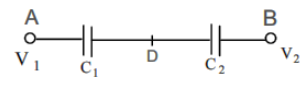
Two capacitors \[{C_1}\] and \[{C_2}\] in a circuit are joined as shown in figure. The potentials of points A and B are \[{V_1}\] and \[{V_2}\] respectively, then the potential of point D will be

A. $\dfrac{1}{2}\left( {{V_1} + {V_2}} \right)$
B. $\dfrac{{{C_1}{V_2} + {C_2}{V_1}}}{{{C_1} + {C_2}}}$
C. $\dfrac{{{C_1}{V_1} + {C_2}{V_2}}}{{{C_1} + {C_2}}}$
D. $\dfrac{{{C_2}{V_1} - {C_1}{V_2}}}{{{C_1} + {C_2}}}$

Answer 1

Hint: The potential difference between two points in a circuit is the difference in the amount of energy that charge carriers have. The potential difference is also known as voltage and is measured in volts (V). To determine the potential difference, we use a voltmeter (or voltage).

Complete step by step answer:
The ratio of the amount of electric charge deposited on a conductor to the difference in electric potential is known as capacitance. Self-capacitance and mutual capacitance are two closely related concepts of capacitance. Self-capacitance is a property of any material that can be electrically charged.

The difference in electric potential between two points, which is defined as the work required per unit of charge to transfer a test charge between the two points, is known as voltage, electric potential difference, electromotive power, electric strain, or electric tension.When matter is put under an electromagnetic field, it acquires an electric charge, which allows it to undergo a force.

Positive and negative charges are the two forms of electric charge. Charges that are similar repel each other, while charges that are dissimilar attract each other. We know that
$q = C V$
Let the potential at $D$ be considered as ‘$V$’.Now the Potential drop across
${C_1} = \left( {V - {V_1}} \right)$
$\Rightarrow {C_2} = \left( {V - {V_2}} \right)$
Hence,
${q_1} = {C_1}\left( {V - {V_1}} \right)$
$\Rightarrow {q_2} = {C_2}\left( {{V_2} - V} \right)$
Since ${q_1} = {q_2}$(This is due to the fact that capacitors are in series]
${C_1}\left( {V - {V_1}} \right) = {C_2}\left( {{V_2} - V} \right)$
$\therefore V = \dfrac{{{C_1}{V_1} + {C_2}{V_2}}}{{{C_1} + {C_2}}}$

Hence, the correct answer is option C.

Note: Only the geometry of the design (for example, the area of the plates and the distance between them) and the permittivity of the dielectric material between the plates of the capacitor determine the capacitance. The permittivity, and hence the capacitance, of certain dielectric materials is independent of the potential difference between the conductors and the overall charge on them.