Question

Two boys A and B pass the same place P on a straight road riding their bicycles in the same direction. The boy A passes P at 7:30:00 AM and moves with uniform velocity of 5 m/s. Another boy B passes the place P some time after A and moves with uniform velocity 10 m/s and overtakes A 500 m away from P, T what time does the boy B passes place P?

Answer 1

Hint: In this question we need to find time at which boy B will pass P, so first of all we need to find time taken by boy a to travel 500 m from P at which boy B will overtake him by which we can calculate our required time.

Formula used:
$T=\dfrac{D}{V}$,

Complete Step by step solution:
Velocity of boy A (${{V}_{A}}$) = 5 m/s,
Velocity of boy B (${{V}_{B}}$) = 10 m/s

Now, Boy A will take time ${{T}_{A}}$ to cover 500 m so,
${{T}_{A}}=\dfrac{D}{V}$ here D is distance(500 m) and V is velocity(5 m/s).
${{T}_{A}}=\dfrac{500}{5}=100\sec $

Now, when B overtakes A,

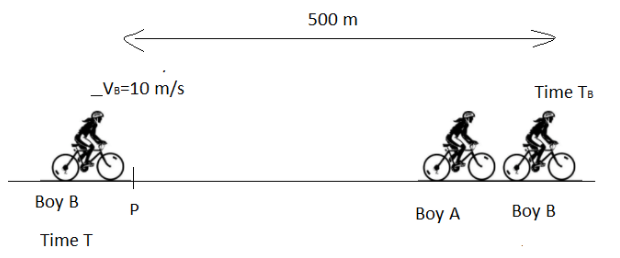
We need to calculate time T at which boy B passes P, for that first we need to calculate time ${{T}_{B}}$at which B passes A after that we need to subtract ${{T}_{B}}$from ${{T}_{A}}$ by which we can calculate after how much time B passes P .

So, ${{T}_{B}}=\dfrac{D}{V}$
 ${{T}_{B}}=\dfrac{500}{10}=50\sec $

Now, ${{T}_{A}}-{{T}_{B}}=100-50=50\sec $, which means B passes P after 50 sec when A passes P, so to calculate T we have to add 50 sec to the time when A passes P which is 7:30:00 AM,

So, B passes from P at 7:30:50 AM.

Additional information:
We can see that due to high velocity of boy B he can overtake A in some time, if it would be lower than that of boy A then also it will be passing through point A but at some different point of time.

Note:
To solve these type of problems we need to carefully observe the time difference and between both persons t crossing each other and when they are passes through point P to calculate our required answer