Question

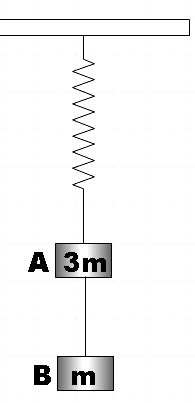
Two blocks A and B of masses 3m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of A and B immediately after the string is cut are respectively:

A.$\dfrac{g}{3},g$
B.$g,g$
C.$\dfrac{g}{3},\dfrac{g}{3}$
D.$g,\dfrac{g}{3}$

Answer 1

Hint: As a first step, you could make a neat free body diagram of the given system. Thereby you will be able to balance the forces acting on each of the blocks. As a second part you could balance the forces acting on the blocks after being cut. Thereby, you could easily find the accelerations of the blocks after being cut.

Complete Step by step solution:
In the question, we are given two blocks A and B of mass 3m and m connected by a string and the whole system is suspended with the help of a massless spring. We are asked to find the acceleration of the blocks A and B just after the string connecting them is cut.

As a first step let us mark all the forces acting on the two blocks and hence the whole system.

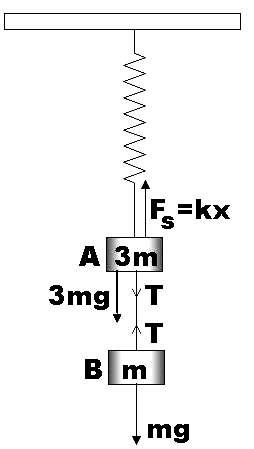
At the initial condition where the whole system is at rest before the string connecting A and B being cut, balancing the forces on blocks A and B would give:
For block B,
$T=mg$ ……………………………………………… (1)
Where, T is the tension in the string.

For block A,
${{F}_{s}}=3mg+T$
Substituting (1),
${{F}_{s}}=3mg+mg$
$\Rightarrow {{F}_{s}}=4mg$ …………………………………………… (2)

Now when the string connecting A and B is cut, the block A would accelerate upward and block B would accelerate downward. So, for block B,
$ma=mg$
$\therefore a=g$ ………………………………… (3)

Now for block A,
${{F}_{s}}-3mg=3ma$
From (2),
$\Rightarrow 4mg-3mg=3ma$
$\Rightarrow mg=3ma$
$\therefore a=\dfrac{g}{3}$ ……………………………………….. (4)
Therefore, we found that the accelerations of the blocks A and B would be $g$ and $\dfrac{g}{3}$ respectively after being cut.

Hence, option D is found to be the correct answer.

Note:
You could imagine a practical example of the given system to realize that the restoring force will pull the block A upwards being cut. The block B will be accelerating downwards due to gravity. We also see that after being cut block B is under free fall and hence the only force on it will be that due to gravity.