Question

Two beams of red and violet colours are made to pass separately through a prism (angle of the prism is ${{60}^{\circ }}$). In the position of minimum deviation, the angle of refraction will be:
A.${{30}^{\circ }}$ for both the colours
B.Greater for the violet colour
C.Greater for the red colour
D.Equal but not ${{30}^{\circ }}$ for both the colours

Answer 1

Hint:In minimum deviation condition, the ray refracted from the air to the prism becomes parallel to the base of the prism. Also, the angle of refraction does not depend on the wavelength of light incident. Therefore, the angle of refraction will be calculated by applying basic geometry related to parallel lines and their intersections.

Complete answer:
The refractive index of prism, $\mu $ is also expressed as:
\[\mu =\dfrac{\sin \left[ \dfrac{A+{{\delta }_{m}}}{2} \right]}{\sin \left[ \dfrac{A}{2} \right]}\]
Where,
$A=$ angle of prism
${{\delta }_{m}}=$ angle of minimum deviation of prism
This formula proves that the angle of refraction and minimum deviation are independent of the wavelength of light.
Since, the refracted ray which was first incident on the surface of prism becomes parallel to the base of the prism, therefore, it also forms a small equilateral triangle like the prism with all three angles equal to ${{60}^{\circ }}$ as shown in figure.

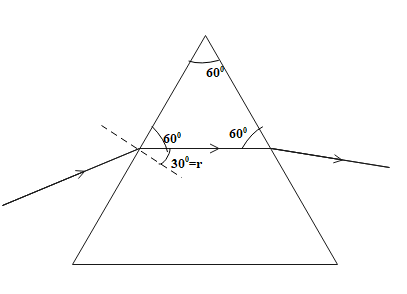
The normal to the surface of the prism makes an angle of ${{90}^{\circ }}$ with the prism. Thus, we get
${{90}^{\circ }}={{60}^{\circ }}+r$
$\Rightarrow r={{30}^{\circ }}$
Therefore, the angle of refraction is ${{30}^{\circ }}$ and since it is independent of wavelength of light, hence the angle of refraction is ${{30}^{\circ }}$for both red and violet colour beams.

Therefore, the correct answer is (A) ${{30}^{\circ }}$ for both the colours.

Note:
For a given prism, the angle of deviation only depends on the angle of incidence. Studying from the angle of incidence equal to zero, as we increase the angle of incidence, the angle of deviation slowly decreases to a minimum value and then shoots up to infinity as we keep increasing the angle of incidence of the light ray. This can be observed easily with the graph of angle of incidence ($i$) v/s angle of deviation ($\delta $).