Question

Two acute angles of a right triangle are equal. Find the two angles.

Answer 1

Hint: A three sided figure is said to be a triangle, it has three angles in total. An acute angle is any angle which has the value of an angular degree that is less than $ {90^ \circ } $ . A right triangle or commonly called as the right angled triangle is a triangle that possesses the value of one of its angles as $ {90^ \circ } $ .
Formula used:
Sum of angles of a triangle is $ {180^ \circ } $ .

Complete step-by-step answer:
Let us note down the given values:

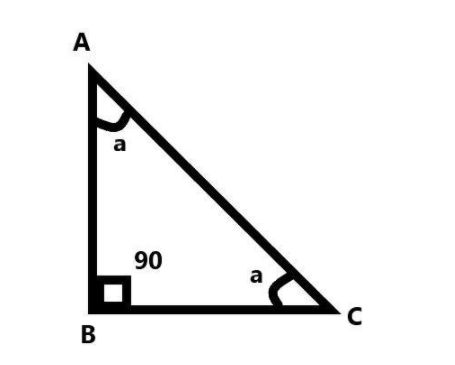
It is given that the triangle says triangle $ ABC $ is right angled so one angle, let it be angle $ B $ it is $ {90^ \circ } $ .
Then for any right triangle, the remaining two angles have to be acute, but they have mentioned that the two acute angles are equal.
So let the acute angles be: $ \angle BAC = \angle BCA = a $
The sum of angular values of every triangle can only be $ {180^ \circ } $ . So we can express the sum of each angle in a triangle as $ {180^ \circ } $ .
The equation would look like:
 $ \Rightarrow \angle ABC + \angle BAC + \angle BCA = {180^ \circ } \to (i) $
Here we already know that: $ \angle BAC = \angle BCA = a $ and $ \angle ABC = {90^ \circ } $ so we substitute these values into the equation $ (i) $ .
Then equation $ (i) $ becomes:
 $ \Rightarrow {90^ \circ } + a + a = {180^ \circ } $
Since there is only a single variable in the above derived equation, we can easily solve it to find the value of the variable $ a $ of that equation. If we find $ a $ ’s value, we will have found the required value of the acute angle.
So solving the equation as follows:
 $ \Rightarrow {90^ \circ } + 2a = {180^ \circ } $
Separate the variable and keep it on one side:
 $ \Rightarrow 2a = {180^ \circ } - {90^ \circ } $
 $ \Rightarrow 2a = {90^ \circ } $
Simplifying further, the value of ‘ $ a $ ’ becomes:
 $ \Rightarrow a = {45^ \circ } $
Therefore the value of each acute angle ( $ a $ ) in the right triangle is $ 45{}^ \circ $ and $ 45{}^ \circ $ .
So, the correct answer is “ $ 45{}^ \circ $ and $ 45{}^ \circ $ .”.

Note: Triangles can have different types of angles, we discussed acute angles and right angles, so another type of angle that can be found in triangles commonly is the obtuse angle. Any angular value greater than $ {90^ \circ } $ but less than $ {180^ \circ } $ is said to be obtuse. Any triangle with an obtuse angle, can only have one obtuse angle and the other two angles must be acute.