Question

How many triangles whose vertices are chosen from the vertices of a cube are equilateral?
A.3
B.2
C.4
D.8

Answer 1

Hint: A cube has four lateral surfaces, one top surface and one bottom surface. We can get an equilateral triangle by joining the opposite ends of vertices that have a common point which is the point where the cube's angle is formed.

Complete step-by-step answer:
We know a cube has four lateral surfaces, one top surface and one bottom surface. Each diagonal of the surfaces of a cube are equal in length. So by using these diagonals we can get equilateral triangles. Let us draw a cube first.

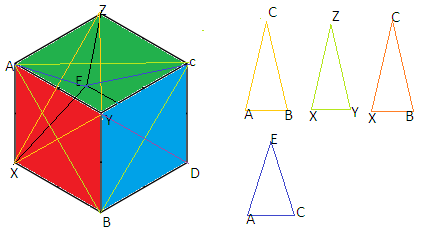
In the above figure AXBY and AYCZ are lateral surfaces. YBDC is the bottom surface and AXEZ is the top surface. Now join the diagonal of the cube. We see that the two lateral surfaces form two triangles ∆ABC with bottom surface and ∆XYZ with top surface.
The two triangles are formed by one pair of adjacent lateral surfaces with bottom and top surface. These two triangles are formed on different planes and the side of each triangle is coplanar.
Here there are a total four pairs of adjacent lateral surfaces and each pair makes $2$ triangles with bottom and top surfaces.
So Total triangles =$4 \times 2$ =$8$
Now, if we flip or change the bottom and top surfaces then again using the same process we obtain $8$ equilateral triangles. But these triangles will be the same as the first $8$ triangles.
So, total $8$ triangles can be formed when vertices of triangles are chosen from the vertices of a cube.
Hence the correct answer is D.

Note: We can also solve this question by marking the top vertices as A, B, C, D and bottom vertices as W, X, Y, Z. Join diagonal AC then ACX and ACZ are two equilateral triangles. Similarly we can obtain two Triangles by joining each diagonal WY, BZ and XZ. So $2 \times 4 = 8$
Hence eight equilateral triangles are obtained.