Question

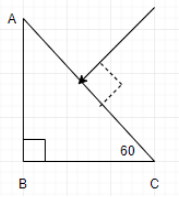
Trace the path of a ray of light passing through a glass prism ABC as shown in the figure. If the refractive index of glass is \[\sqrt{3}\], then find out the value of the angle of emergence from the prism.

Answer 1

Hint:This is a case of the occurrence of refraction, where the light bends when it travels to a medium with a different value of refractive index. In a prism, the deviation takes place twice. Hence to trace the path of light that passes through the prism, we should note the fact that the refracting surfaces of the prism aren’t parallel to each other.

Formulas used:
Formula for Snell’s law:
${{n}_{1}}\sin {{\theta }_{1}}={{n}_{2}}\sin {{\theta }_{2}}$
Where ${n_1}$ is the refractive index of the incident medium, ${n_2}$ is the refractive index of the refracting medium, ${{\theta }_{1}}$ is the angle of incidence and ${{\theta }_{2}}$ is the angle of refraction.

Complete step by step answer:
Refractive index of a medium can be defined as the phenomenon where light bends when it travels from one medium to another, with variation in refractive index. Refraction in a glass prism does not involve parallel surfaces. Thus, refraction occurs twice in a prism. The first time is when the ray enters the prism and the second time when the ray emerges out of the prism.

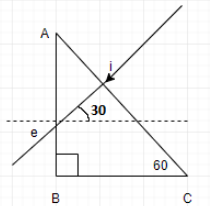
We know that according to Snell’s law,
${{n}_{1}}\sin {{\theta }_{1}}={{n}_{2}}\sin {{\theta }_{2}}$
Or ${{n}_{a}}\sin i={{n}_{g}}\sin r$
\[{{n}_{g}}=\sqrt{3},i=0\] (given)
$
\sin i=\sin 0=0 \\
\Rightarrow r=0 \\
$
At the surface AB, $i={{30}^{\circ }}$(geometrically)
Thus we apply the Snell’s law again to find the angle of emergence e
$
\dfrac{\sin {{30}^{\circ }}}{\sin e}=\dfrac{{{n}_{a}}}{{{n}_{b}}}=\dfrac{1}{\sqrt{3}} \\
\Rightarrow \sin e=\sqrt{3}\sin {{30}^{\circ }} \\
\therefore e={{60}^{\circ }} \\
$
Hence the value of the angle of emergence is ${{60}^{\circ }}$.

Note:Refraction through a prism is entirely different from that of a glass slab because here, the incident light is not parallel to the emergent light and it bends towards the base of the prism. Also, the phenomenon of dispersion takes place in the glass prism and not in the glass slab because of the complete variation in the construction and geometry of both of those. Hence, the light emerges out in totally different methods and the corresponding questions are to be approached in different manners because through the material is same, the construction is different.