Question

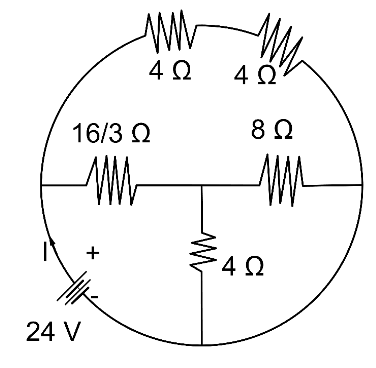
What is the total current supplied by the battery to the circuit shown in the following figure?

A. $2{\text{ }}A\:$
B. $4{\text{ }}A\:$
C. $6{\text{ }}A\:$
D. \[9{\text{ }}A\]

Answer 1

Hint: We will first evaluate the equivalent resistance of the circuit. Then we will use the formula of ohm’s law to evaluate the current through the circuit with the help of basic formulae..

Formulae Used:
${R_{Series}}{\text{ }} = {\text{ }}{R_1}{\text{ }} + {\text{ }}{R_2}{\text{ }} + {\text{ }}....{\text{ }} + {\text{ }}{R_n}$
\[\Rightarrow \dfrac{1}{{{R_{Parallel}}}}{\text{ }} = {\text{ }}\dfrac{1}{{{R_1}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_2}}}{\text{ }} + {\text{ }}....{\text{ }} + {\text{ }}\dfrac{1}{{{R_n}}}\]
$\Rightarrow I{\text{ }} = {\text{ }}\dfrac{V}{R}$

Complete step by step answer:
We will discuss the ohm’s law a bit in detail. An experiment was performed to evaluate a relation between current and potential differences. It was observed that
\[V{\text{ }} \propto {\text{ }}I\]
A proportionality constant $R$ was introduced. Thus, the equation evaluated was
$V{\text{ }} = {\text{ }}RI$
$R$ is known as the resistance of the circuit which is simply defined as the opposition offered by any conductor to flowing charges in it. Now, the ohm’s law was defined as the potential difference across a circuit that is directly proportional to the current flowing through the circuit at constant temperature.
Let, ${R_1}{\text{ }} = {\text{ }}4{\text{ }}\Omega $
$\Rightarrow {R_2}{\text{ }} = {\text{ }}4{\text{ }}\Omega $
$\Rightarrow {R_3}{\text{ }} = {\text{ }}\dfrac{{16}}{3}{\text{ }}\Omega $
$\Rightarrow {R_4}{\text{ }} = {\text{ }}4{\text{ }}\Omega $
$\Rightarrow {R_5}{\text{ }} = {\text{ }}8{\text{ }}\Omega $
Now,
${R_1}$ and ${R_2}$ are in series
Thus,
${R_{Up}}{\text{ }} = {\text{ }}{R_1}{\text{ }} + {\text{ }}{R_2}$
Substituting the values, we get
${R_{Up}}{\text{ }} = {\text{ }}4{\text{ }} + {\text{ }}4{\text{ }} = {\text{ }}8{\text{ }}\Omega $
Now,
${R_4}$ and ${R_5}$ are in parallel
Thus,
$\dfrac{1}{{{R_{Mid}}}}{\text{ }} = {\text{ }}\dfrac{1}{{{R_4}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_5}}}$
Substituting the values, we get
$\dfrac{1}{{{R_{Mid}}}}{\text{ }} = {\text{ }}\dfrac{1}{4}{\text{ }} + {\text{ }}\dfrac{1}{8}{\text{ = }}\dfrac{3}{8}$

Further, we get
${R_{Mid}}{\text{ }} = {\text{ }}\dfrac{8}{3}{\text{ }}\Omega $
Now,
${R_{Mid}}$ and ${R_3}$ are in series
Thus,
${R_{central}}{\text{ }} = {\text{ }}{R_{Mid}}{\text{ }} + {\text{ }}{R_3}$
Substituting the values, we get
${R_{central}}{\text{ }} = {\text{ }}\dfrac{8}{3}{\text{ }} + {\text{ }}\dfrac{{16}}{3}{\text{ }} \\
\Rightarrow {R_{central}}{\text{ }} = {\text{ }}\dfrac{{24}}{3}{\text{ }} \\
\Rightarrow {R_{central}}{\text{ }} = {\text{ }}8{\text{ }}\Omega $
Now, ${R_{central}}$ and ${R_{Up}}$ are in parallel

Thus,
$\dfrac{1}{{{R_{eq}}}}{\text{ }} = {\text{ }}\dfrac{1}{{{R_{central}}}}{\text{ }} + {\text{ }}\dfrac{1}{{{R_{Up}}}}$
Substituting the values, we get
$\dfrac{1}{{{R_{eq}}}}{\text{ }} = {\text{ }}\dfrac{1}{8}{\text{ }} + {\text{ }}\dfrac{1}{8}{\text{ }} \\
\Rightarrow \dfrac{1}{{{R_{eq}}}}{\text{ }} = {\text{ }}\dfrac{1}{4}$
Thus, we get
${R_{eq}}{\text{ }} = {\text{ }}4{\text{ }}\Omega $
Now,
According to ohm’s law, we know
$I{\text{ }} = {\text{ }}\dfrac{V}{{{R_{eq}}}}$
Putting in the values, we get
$I{\text{ }} = {\text{ }}\dfrac{{24}}{4}$
Further, we get
$\therefore I{\text{ }} = {\text{ }}6{\text{ }}A$

Hence, the correct answer is C.

Note: Students should be very cautious while judging the type of combination of resistors. Students often make mistakes while putting in the final resistance calculated of a parallel combination as the formula is of a reciprocated type. Thus, they should be very cautious while doing the same.