Question

To get an output of 1. from the circuit shown in the figure the input must be

A. $a = 0,b = 0,c = 1$
B. $a = 1,b = 0,c = 0$
C. $a = 1,b = 0,c = 1$
D. $a = 0,b = 1,c = 0$

Answer 1

Hint: The language which we use is completely different from computer language. It is called binary language and there will be only two numbers and the computer will understand any information in that to numbers. They are called binary digits which are 0 and 1. The inputs and outputs from the logic gates are given and obtained in those binary digit form only.

Complete step-by-step solution:
The logic gates which we use are the basic requirements for any electronic circuits. In the case of logic gates generally, there will be one or more inputs and there will be only one output. There is entire logic processed between those inputs to get the output.
It is just like any function. For example, consider the integral function. We will give some input. Then that input is processed over the function called integration and finally, we will get some output.
Similarly here we give inputs in the form of binary digits 0 and 1. These are processed by some logic due to these logic gates and finally, we will get some output.
Frequently used logic gates are OR gate, AND gate, NOT gate, NOR gate, NAND gate.
If we refer to the diagram below the gates given are OR, AND.

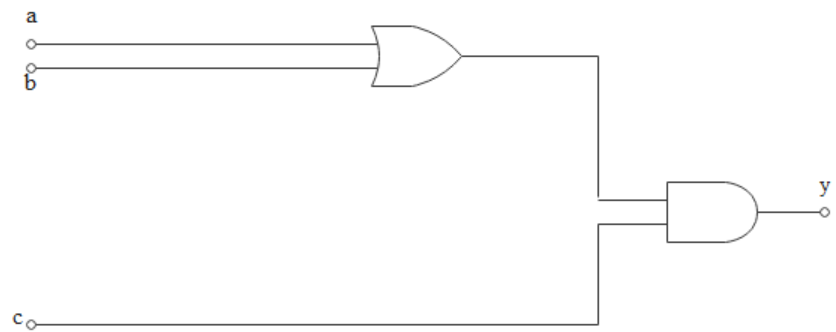
let a,b are two inputs for OR gate. Then the operation is generally denoted by
a OR b = $a + b$
Except for a=0, b=0 for all the rest values the output will be 1.
let a,b are two inputs for AND gate. Then the operation is generally denoted by
a AND b = $a.b$
Except for a=1, b=1 for all the rest values the output will be 0.
Now in the given diagram, a,b are processed by the OR gate. So in order to get output as 1 we can have a=1, b=0 or a=0, b=1 or a=1, b=1
But the final output(y) after the AND gate must be 1. So input ‘c’ must be definitely equal to 1. So c=1 is fixed.
Now the only option satisfying the above criteria is $a = 1,b = 0,c = 1$. Hence option C will be the answer.

Note: The plus symbol which we had used in the OR gate is not the general arithmetic plus symbol. It’s a binary operation. The dot we had used in the AND gate is not a DOT product. It is the binary operation for the AND gate. NAND and NOR gates are called universal gates.