Question

To get an $OR$ gate from a $NAND$ gate, we need:
A) Only two $NAND$ gates.
B) Two $NOT$ gates obtained from $NAND$ gates and one $NAND$ gate.
C) Four $NAND$ gates and two $AND$ gates obtained from $NAND$ gates.
D) None of the above.

Answer 1

Hint:
Boolean algebra needed:
1) Involution law: $\left( {X'} \right)' = X$
2) Idempotency law:
$
  X + X = X \\
  X.X = X \\
 $
3) De-Morgan’s law:
$
  \left( {X + Y} \right)' = X'.Y' \\
  \left( {X.Y} \right)' = X' + Y' \\
 $

Complete step by step answer:
Construct a $NOT$ gate using $NAND$ gate. For this, you will need to use idempotency law.
Connect $NOT$ gates to two terminals and connect a $NAND$ gate. Then, by using idempotency law, arrive at the result that you can also get simply by using $OR$ gate.
Complete step by step answer:
We will be using three laws of Boolean algebra. These are:
1) Involution law: $\left( {X'} \right)' = X$
2) Idempotency law:
$
  X + X = X \\
  X.X = X \\
 $
3) De-Morgan’s law:
$
  \left( {X + Y} \right)' = X'.Y' \\
  \left( {X.Y} \right)' = X' + Y' \\
 $
Our first step will be to make a $NOT$ gate using $NAND$ gate.
The symbol and result of $NOT$ gate is :$$
 

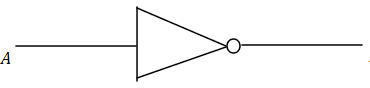
$NOT$ gate using $NAND$ gate is:

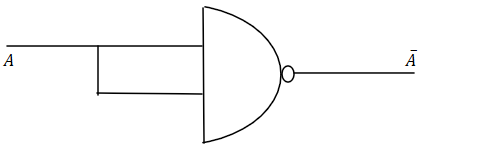
We will explain this construction using Idempotency law ( $X.X = X$ )
$A$ can be written as $A.A$ and vice versa. $\left( {A.A} \right)' = \left( A \right)'$ because we are using $NAND$ gate.
Our, desired gate is $OR$ gate, which is represented as

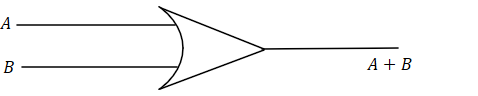
Our desired result is $A + B$. First using Involution law ( $\left( {X'} \right)' = X$ ), we get
$A + B = \left[ {\left( {A + B} \right)'} \right]'$ and then using De-Morgan’s law, we get $\left[ {\left( {A + B} \right)'} \right]' = \left[ {A'.B'} \right]'$
So, we have $\left[ {\left( {A + B} \right)'} \right]' = \left[ {A'.B'} \right]'$. Now, using Idempotency law ( $X.X = X$ ), we have
$\left[ {A'.B'} \right]' = \left[ {\left( {A.A} \right)'.\left( {B.B} \right)'} \right]'$
So, we have the entire expression as
$A + B = \left[ {\left( {A.A} \right)'.\left( {B.B} \right)'} \right]'$
From this expression, we can conclude that we need two $NOT$ gates using $NAND$ gates and then combine then using $NAND$ gate to get the desired results.

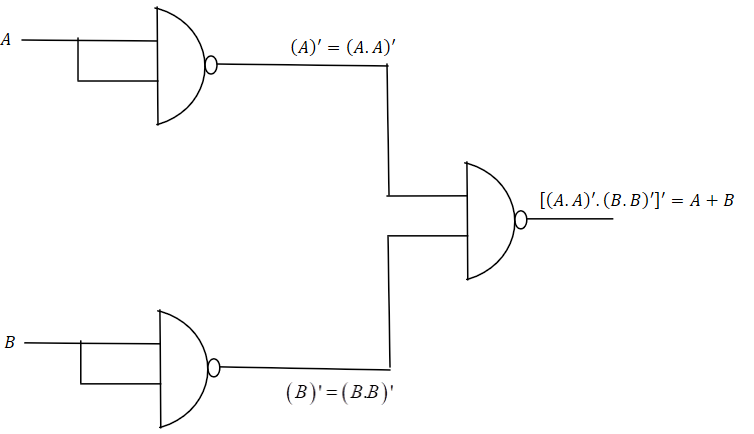
So, option C is correct.

Note:You can match your answers by comparing the truth tables. To construct different gates easily, one should be familiar and comfortable in any Boolean algebra laws. Do not get confused with symbols for different gates.