Question

To divide a line segment AB in the ratio 4:7, a ray AX is drawn first such that $\angle BAX$ is an acute angle and then points ${A_1},{A_2},{A_3}............$ are located at equal distances on the ray AX. The point B is joined to:
A. ${A_{12}}$
B. ${A_{11}}$
C. ${A_{10}}$
D. ${A_9}$

Answer 1

Hint- In order to solve this question, first we will draw the line segment AB and then we want to divide the line in the ratio 4:7, so we will take the sum so the ratio and then divide the sum by the total number of ratios to get the result.

Complete step-by-step answer:
First draw line AB as shown in figure.

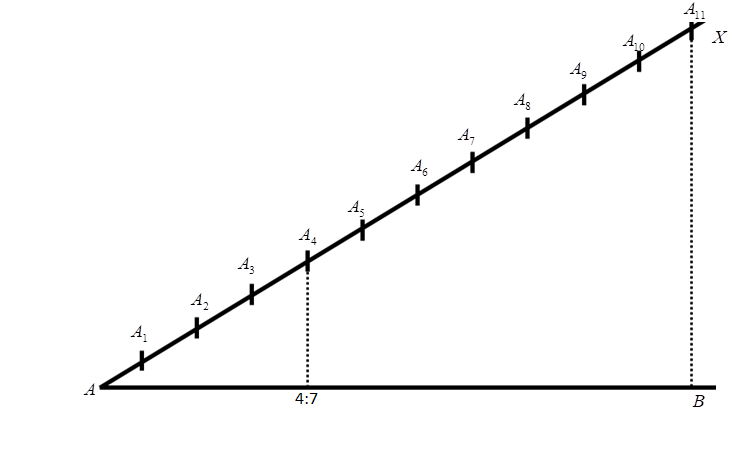
Now take point A on the AB ray and make an acute angle less than 90 degree such that angle BAX is an acute angle.
Now, divide the line AX into 7+4=11 parts such that they are at equal distance and are marked as
${A_1},{A_2},{A_3}............$
To divide the line AB in ratio 4:7, from ${A_4}$ on the line AX, draw line perpendicular to AB and join them.
Similarly, from ${A_{11}}$ on the line AX, draw a line perpendicular of AB and at point B.
Therefore the point ${A_{11}}$ is joined to the point B.
Hence, the correct option is B.

Note- In order to solve these types of questions related to construction, remember the steps of construction and know how to draw a line perpendicular to another line, how to make an acute angle. In this question we have divided the line AB into the asked ratio 4:7 with the help of another line.