Question

To construct a triangle ABC in which BC = 10cm and $\angle B={{60}^{\circ }}$ and AB+AC = 14cm, then the length of BD used for construction is
\[\begin{align}
  & A.7cm \\
 & B.14cm \\
 & C.20cm \\
 & D.10cm \\
\end{align}\]

Answer 1

Hint: In this question, we need to find the length of BD which is used for constructing triangle ABC. In triangle ABC, we have BC = 10cm, $\angle B={{60}^{\circ }}$ and AB+AC = 14cm. We will construct triangle ABC using given measures and then find the length of BD using isosceles triangle property. According to the isosceles triangle property, the angles corresponding to equal sides are also equal.

Complete step-by-step solution
Let us construct triangle ABC in which BC = 10cm, $\angle B={{60}^{\circ }}$ and AB+AC = 14cm. We will use following steps of construction:
(i) Draw line segment BC = 10cm. At B, let us draw an angle, say $\angle XBC$ which is equal to ${{60}^{\circ }}$ using a protractor.

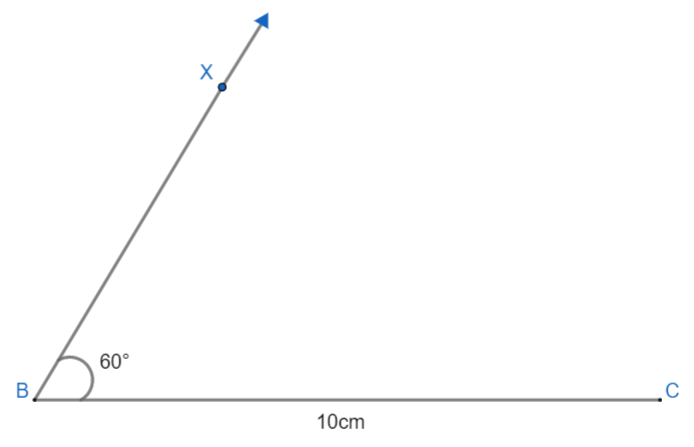
(ii) Now, cut the ray BX at the length of AB+AC = 14cm at point D (open compass at 14cm and cut the ray and mark the point as D). And then join DC.

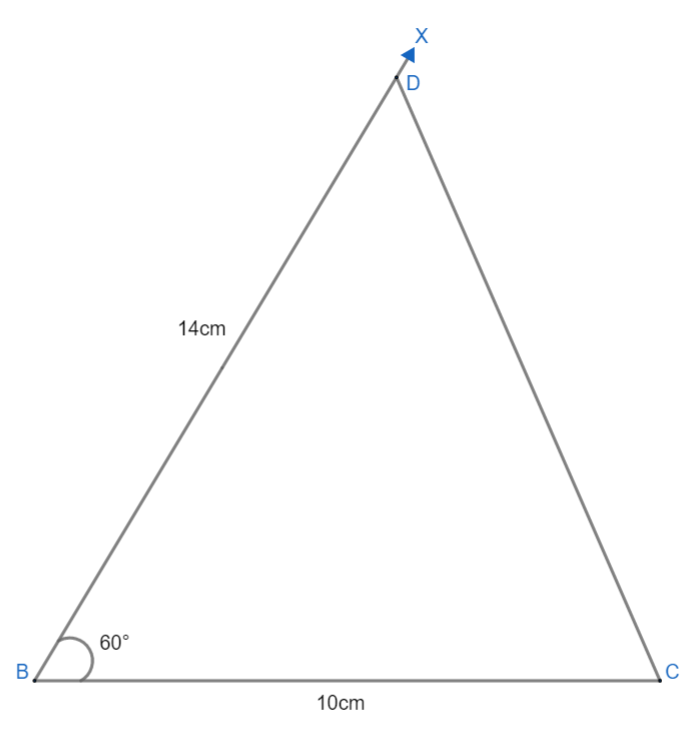
(iii) Now, measure $\angle BDC$ and make the same angle at C naming DCY. Ray CY cuts the line BD at point A.

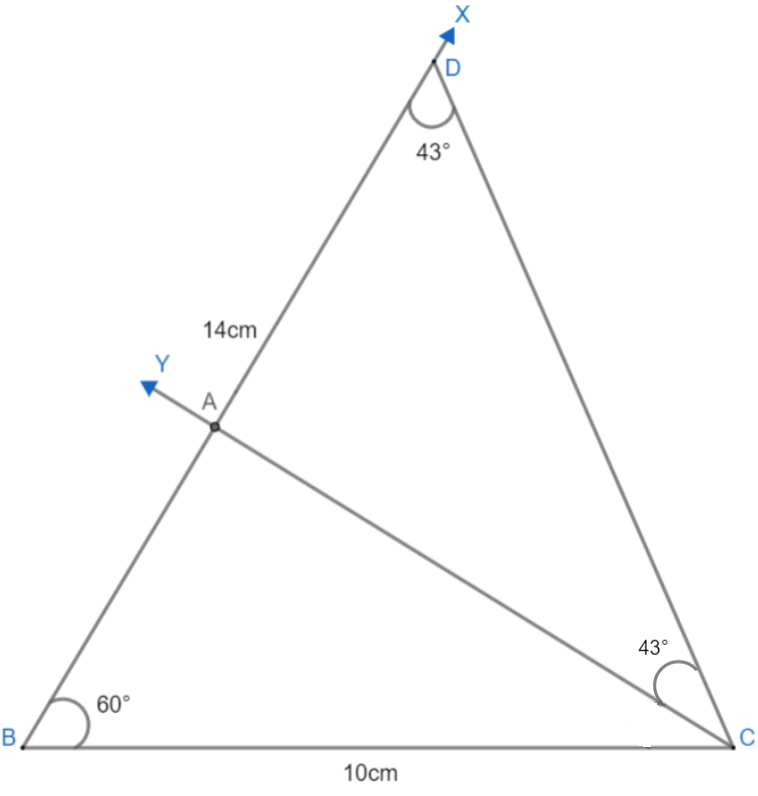
Hence, $\Delta ABC$ is the required triangle with BC = 10cm, AB+AC = 14cm and $\angle B={{60}^{\circ }}$.
Now, we need to find the length BD. Since BD was already drawn as 14cm so BD = 14cm.
But let us prove BD as 14cm.
From $\Delta ACD$ we can see that, $\angle ADC=\angle DCA$.
Hence, $\Delta ACD$ is an isosceles triangle.
So, AD = AC by the reverse of isosceles triangle property.
We know that, AB+AC = 14cm. Putting AD = AC we get: AB+AD = 14cm.
From the diagram, we can see that AB+AD = BD.
Hence, BD = 14cm.
Hence, option B is the correct answer.

Note: Students should take care while measuring the angle $\angle BDC$. When drawing angle $\angle DCY$ make sure to take base as CD and then measure the angle using a protractor. For making an angle of ${{60}^{\circ }}$ students can use a protractor or compass. Make sure pencils are sharp and the compass is tight.