Question

Through two parallel wires A and B, 10A and 2A of currents are passed respectively in opposite directions. If the wire A is infinitely long and the length of the wire B is 2m, then force on the conductor B, which is situated at 10cm distance from A, will be
A. $8 \times {10^{ - 7}}N$
B. $8 \times {10^{ - 5}}N$
C. $4 \times {10^{ - 7}}N$
D. $8 \times {10^{ - 5}}N$

Answer 1

Hint: The force between two long straight and parallel conductors separated by a distance ‘r’ is found by applying ampere’s circuital law. Ampere’s circuital law states that the line integral of the magnetic field surrounding a closed loop is equal to the number of times of the algebraic sum of the currents passing through the loop.

Formula used:
$F = \dfrac{{{\mu _ \circ }}}{{4\pi }}\dfrac{{2{I_1}{I_2}}}{r} \times l$

Complete answer:
Let us assume two wires carrying current ‘${I_1}$’ and ‘${I_2}$’ and the field produced by the first wire and the force exerted on the second wire known as force ‘${F_2}$’.
Now, the field due to ‘${I_1}$’ at a distance ‘r’ is given as,
${B_1} = \dfrac{{{\mu _ \circ }{I_1}}}{{2\pi r}}$
This resulted field is uniform along the second wire and perpendicular to it, so the force ‘${F_2}$’ exerted on second wire is given as,
$F = IB\sin \theta $
$ \Rightarrow {F_2} = {I_2}l{B_1}$ ; $\sin \theta = 1$
So, by Newton’s third law the forces on the wires are equal in magnitude. We can write ‘F’ for the magnitude ‘${F_2}$’.
The force between two parallel currents ‘${I_1}$’ and ‘${I_2}$’, is separated by a distance ‘r’, has a magnitude per unit length which is given by
$\dfrac{F}{l} = \dfrac{{{\mu _ \circ }{I_1}{I_2}}}{{2\pi r}}$
According to this, the force is said to be attractive when the currents are in the same direction, and is repulsive if they are in the opposite directions.
In order to find the solution of the given question let's draw a rough diagram for a better understanding of the question, and apply the formula of the force between two parallel current carrying wires.

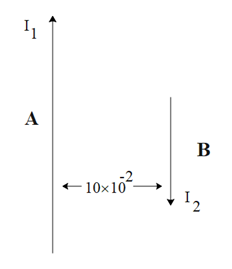
$F = \dfrac{{{\mu _ \circ }}}{{4\pi }}\dfrac{{2{I_1}{I_2}}}{r} \times l$
$ \Rightarrow F = \dfrac{{{{10}^{ - 7}} \times 2 \times 10 \times 2}}{{0.1}} \times 2$
On calculating we get,
$ \Rightarrow F = 8 \times {10^{ - 5}}N$

So, the correct answer is “Option D”.

Note:
We can find the definition of ampere from the above explained concept. One ampere is defined as the current through each of the two parallel conductors of infinite length which is separated by a distance of one meter in a space which is free of other magnetic fields and causes a force of exactly $2 \times {10^{ - 7}}N/m$ on each of the conductors.