Question

Three vertices of a rectangle are $A\left( 2,-1 \right)$, $B\left( 2,7 \right)$ and $C\left( 4,7 \right)$. Plot these points on a graph and hence use it to find:
 (i) coordinates of fourth vertex D.
Also, find the coordinates of (ii) the midpoint of the CD.
What is the area of the rectangle?

Answer 1

Hint: We will first draw a rectangle with the help of given three coordinates on the graph. Examining the graph, we will find the fourth coordinate. Similarly, we will find the midpoint of CD using a graph or midpoint formula. At last to calculate the area of the rectangle we will require length and breadth of rectangle because area of rectangle = length x breadth. We will find length and breadth using distance formulas between coordinates. Distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].

Complete step-by-step solution
Let us draw a graph using three coordinates and drawing perpendicular lines to find coordinates of D.

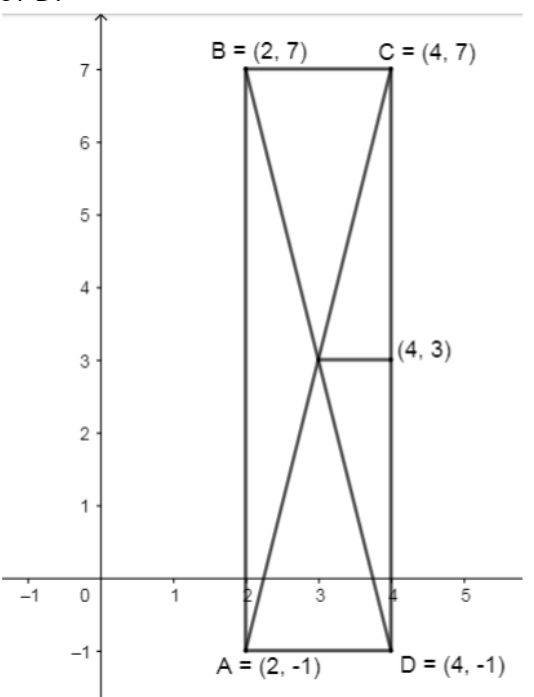
As from the graph, we can see that coordinates of D are $\left( 4,-1 \right)$. Now let us use the midpoint formula to find the midpoint of CD.
Coordinates of C are $\left( 4,7 \right)$ and coordinates of D are $\left( 4,-1 \right)$.
Midpoint of CD is given by
$\begin{align}
  & \left( \dfrac{4+4}{2},\dfrac{7-1}{2} \right) \\
 & =\left( \dfrac{8}{2},\dfrac{6}{2} \right) \\
 & =\left( 4,3 \right) \\
\end{align}$
Hence, the midpoint of CD is $\left( 4,3 \right)$.
Now, we have to calculate the area of the rectangle. For that, we have to find the length and breadth which is given by distances between AB and BC.
Using distance formula on AB, we get –
$\begin{align}
  & AB=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} \\
 & =\sqrt{{{\left( 2-2 \right)}^{2}}+{{\left( 7-\left( -1 \right) \right)}^{2}}} \\
 & =\sqrt{{{\left( 8 \right)}^{2}}} \\
 & =8 \\
\end{align}$
Using distance formula on BC, we get –
$\begin{align}
  & AB=\sqrt{{{\left( 4-2 \right)}^{2}}+{{\left( 7-7 \right)}^{2}}} \\
 & =\sqrt{{{\left( 2 \right)}^{2}}} \\
 & =2 \\
\end{align}$
Hence, length $=8units$ and breadth $=2units$.
The area of the rectangle is given by length x breadth. Therefore,
Area of rectangle $=8\times 2=16~square~units$.

Note: Students should carefully mark points on graphs. Lines must be perpendicular to obtain an accurate value of point D. Students can also check coordinates of D by measuring the distance between CD and AB and checking them if they are equal. The midpoint of the CD can also be found with the help of the graph. It is important to mark the X and Y-axis on the graph. To find midpoint through the graph, draw diagonals and then draw lines from the center to CD to obtain the point on CD.