Question

Three point charges $+q,-2q,+q$ are placed at points $(x=0,y=a,z=0)$,$(x=0,y=0,z=0)$, $(x=a,y=0,z=0)$ respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are:
(A).$\sqrt{2}qa$ along +y direction
(B). $\sqrt{2}qa$ along the line joining the points $(x=0,y=0,z=0)$
and $(x=a,y=a,z=0)$.
(C). $qa$ along the line joining the points $(x=0,y=0,z=0)$
and $(x=a,y=a,z=0)$.
(D). $\sqrt{2}qa$ along +x direction

Answer 1

Hint: Dipole moments are the product of magnitude of charge and the distance between them, they are vector quantities. The figure shows two dipoles aligned perpendicular to each other as they are along the perpendicular axis. We can use vector laws of addition to calculate the resultant dipole as well as the direction of resultant.

Formulas used:
$P=qd$
$P'=\sqrt{P_{1}^{2}+P_{2}^{2}+2{{P}_{1}}{{P}_{2}}\cos \theta }$

Complete answer:
A dipole is made of two opposite charges and the dipole moment is defined as the product of magnitude of charge and the distance between them. Its SI unit is $Cm$.
$P=qd$
Here, $P$ is the dipole moment
$q$ is the magnitude of charge
$d$ is the distance between their charges
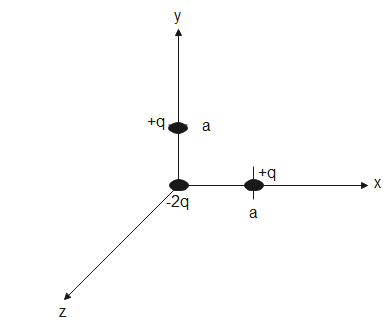
As given, $+q$ is placed on the point $(x=0,y=a,z=0)$, $-2q$ is placed on the point $(x=0,y=0,z=0)$ and another $+q$ is placed on $(x=a,y=0,z=0)$
The charges are placed as shown

We can make dipoles from the charges as-

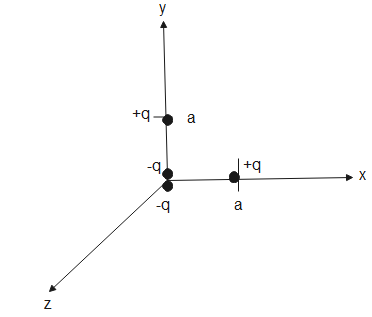
The dipole moment of each dipole will be-
$P=qa$
The dipole moment is a vector quantity. Therefore, we can apply the vector formula to calculate the resultant of the two dipoles.
$P'=\sqrt{P_{1}^{2}+P_{2}^{2}+2{{P}_{1}}{{P}_{2}}\cos \theta }$
Here, $P'$ is the resultant dipole
${{P}_{1}},\,{{P}_{2}}$ are the two dipole moments
$\theta $ is the angle between the dipole moments
For the dipoles given in the figure, ${{P}_{1}}={{P}_{2}}=P=qa$, $\theta ={{90}^{o}}$
Substituting values in the above equation, we get,
$\begin{align}
  & P'=\sqrt{{{(qa)}^{2}}+{{(qa)}^{2}}2(qa)(qa)\cos 90} \\
 & \Rightarrow P'=qa\sqrt{2} \\
\end{align}$
Therefore, the resultant dipole moment is $qa\sqrt{2}$

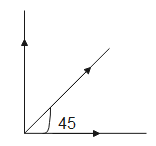
The resultant makes 45 degrees with the dipole. Therefore it is along the line
$\begin{align}
  & y-mx=0 \\
 & \Rightarrow y-\tan 45x=0 \\
 & \therefore y-x=0 \\
\end{align}$
The direction of resultant is along the line, $y-x=0$. It passes through the points $(x=0,y=0,z=0)$ and $(x=a,y=a,z=0)$.
Therefore, the resultant dipole moment is $qa\sqrt{2}$ and its resultant is along the line joining the points $(x=0,y=0,z=0)$ and $(x=a,y=a,z=0)$.

Hence, the correct option is (B).

Note:
The dipole moment is a vector quantity while the charge and distance are scalar quantities. The above method used for calculating the resultant of dipoles is called the parallelogram law of vector addition. The direction from positive charge to negative charge is the direction of a dipole moment.