Question

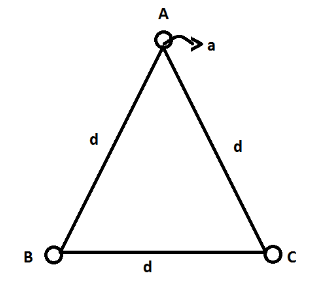
Three identical metallic uncharged spheres \[A,{\text{ }}B,{\text{ }}and{\text{ }}C\] each of the radius a, kept at the corners of an equilateral triangle of side \[d(d \gg a)\] as shown in the figure. The fourth sphere (of radius\[a\]), which has a change in\[q\], touches A and then moves to a position far away. Bis earthed and then the earth connection is removed C is then earthed. The charge on C is:

(A) \[\dfrac{{qa}}{{2d}}(\dfrac{{2d - a}}{{2d}})\]
(B) \[\dfrac{{qa}}{{2d}}(\dfrac{{2d - a}}{d})\]
(C) \[ - \dfrac{{qa}}{{2d}}(\dfrac{{d - a}}{d})\]
(D) \[\dfrac{{qa}}{{2d}}(\dfrac{{d - a}}{{2d}})\]

Answer 1

Hint:If a charged metallic sphere contacts the same size of metallic sphere, then half of the charge is transferred to another one.If a metallic sphere is earthed, then the net potential on that sphere has become zero. There is a charge dislocation in the earthed sphere by the influence of other charges nearby.

Complete step by step answer:
Initially, there are no charges in A, B, C, spheres. So-net charge \[{q_{net}} = 0\]
Then there is a fourth sphere comes in contact with sphere A
So the charge is transferred to A by an amount of \[q/2\]
\[{q_A} = q/2\]
Then removed the fourth sphere and earthed the B sphere. (Indicates figure B)
Because of earthed net Potential at B, \[{V_{net}} = 0\] and there is a charge \[q'\] on B.
\[{V_{net}} = {V_A} + {V_B}\]

\[{V_{net}} = \dfrac{{k{q_A}}}{{{r_A}}} + \dfrac{{k{q_B}}}{{{r_B}}}\]
\[{r_A}\] Distance between centre of the sphere A and centre of the sphere B, \[{r_A} = a + d + a = d + 2a\] but \[d \gg a\] so \[{r_A} = d + 2a = d\].
\[{V_A}\] Is the potential due to the sphere A.
\[{V_B}\] Is the potential due to the charge dislocation in B.
\[k\] is a constant.
\[{V_{net}} = \dfrac{{k(q/2)}}{d} + \dfrac{{kq'}}{a} = 0\]
\[\dfrac{{kq}}{{2d}} = \dfrac{{ - kq'}}{a}\], then \[q' = \dfrac{{ - qa}}{{2d}}\]this is the charge on B.
Now, earth connection removed from B and earthed C
So, net potential on C =0 \[V{'_{net}} = 0\]
\[V{'_{net}} = {V_A} + {V_B} + {V_C} = 0\]
We already know \[{V_A}\]and \[{V_B}\] and substitute values.
\[0 = \dfrac{{k{q_{}}}}{{2d}} + \dfrac{{ - kqa}}{{2{d^2}}} + \dfrac{{k{q_C}'}}{a}\]
Cancel all \[k\]
\[\dfrac{{k{q_{}}}}{{2d}} + \dfrac{{ - kqa}}{{2{d^2}}} = - \dfrac{{k{q_C}'}}{a}\]
\[\dfrac{{{q_{}}}}{{2d}} + \dfrac{{ - qa}}{{2{d^2}}} = - \dfrac{{{q_C}'}}{a}\]
\[(\dfrac{{{q_{}}}}{{2d}} + \dfrac{{ - qa}}{{2{d^2}}})a = - {q_C}'\]
 The charge on C is
\[{q_C}' = - \dfrac{{qa}}{{2d}}[\dfrac{{d - a}}{d}]\]
So the answer is (C) \[ - \dfrac{{qa}}{{2d}}(\dfrac{{d - a}}{d})\]

Note:Earthed means is the grounding of the metallic sphere. We should count this term \[2a\] in \[d + 2a\], if this \[d \gg a\] is not given. Earthling is used in electrical appliances to prevent electric shock by providing a path of unwanted charge flow.