Question

Three identical metallic plates are kept parallel to one another at separation a and b as shown in figure. The outer plates are connected by a thin conducting wire and a charge Q is placed on the central plate. Find the charge on all the six surfaces.

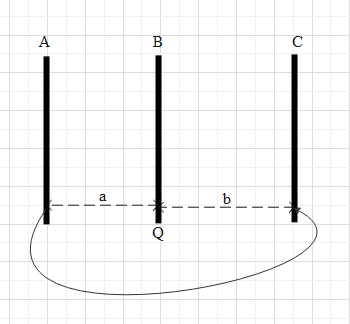
Answer 1

Hint: The given combination of the metal pates is similar to two capacitors in parallel connection with plates A-B and B-C respectively. Find the capacitance of the two capacitors. Then find the relation between the charge on the capacitors and the capacitance.

Complete answer:
The charge Q on the plate B will induce some charge on the each surface of the other two metal plates. The surfaces that are opposite to each other will have equal magnitude of charge but opposite in nature (meaning one positive and one negative).
Let us name the surfaces as 1, 2, 3, 4, 5 and 6. Let the charges on the surfaces 3 and 4 be ${{Q}_{1}}$ and ${{Q}_{2}}$ respectively. Then the charges on 2 and 5 will be $-{{Q}_{1}}$ and $-{{Q}_{2}}$, as shown in the figure.

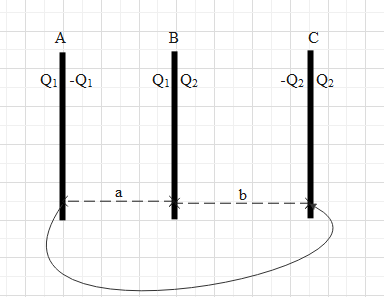
Since the net charge on the plates A and C is zero. The charge on 1 and 6 will be ${{Q}_{1}}$ and ${{Q}_{2}}$ respectively.
Now it is given that the plates A and C are connected by a wire. This means that these two plates have the same potential. Let the potential of plate B be V.
Therefore, we consider this system as two capacitors connected in parallel connection (A-B and B-C).

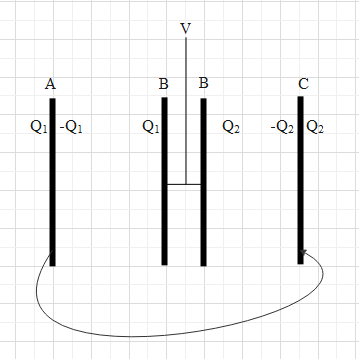
Let the capacitance of A-B be ${{C}_{1}}$ and the capacitance of B-C be ${{C}_{2}}$.
The capacitance is given as $C=\dfrac{A{{\varepsilon }_{0}}}{d}$, where A is the area of cross sectional of the plate, ${{\varepsilon }_{0}}$ is permittivity of free space (a constant) and d is the perpendicular distance between the two plates.
In this case, all the three plates have equal area of cross section.
Therefore, ${{C}_{1}}=\dfrac{A{{\varepsilon }_{0}}}{a}$ ….. (i).
And
${{C}_{2}}=\dfrac{A{{\varepsilon }_{0}}}{b}$ ….. (ii).
We also know that $Q=CV$, where Q is the positive charge on the capacitor and V is the potential difference across the capacitor.
Since both the capacitors are in parallel, the potential difference across is equal.
Therefore, ${{Q}_{1}}={{C}_{1}}V$
And
${{Q}_{2}}={{C}_{2}}V$.
$\Rightarrow \dfrac{{{Q}_{1}}}{{{C}_{1}}}=\dfrac{{{Q}_{2}}}{{{C}_{2}}}$.
Substitute the value of ${{C}_{1}}$ and ${{C}_{2}}$ from (i) and (ii).
$\Rightarrow \dfrac{{{Q}_{1}}}{\dfrac{A{{\varepsilon }_{0}}}{a}}=\dfrac{{{Q}_{2}}}{\dfrac{A{{\varepsilon }_{0}}}{b}}$
$\Rightarrow a{{Q}_{1}}=b{{Q}_{2}}$ …. (iii)
But ${{Q}_{1}}+{{Q}_{2}}=Q$
$\Rightarrow {{Q}_{1}}=Q-{{Q}_{2}}$
Substitute this value in (iii)
$\Rightarrow a\left( Q-{{Q}_{2}} \right)=b{{Q}_{2}}$
$\Rightarrow aQ-a{{Q}_{2}}=b{{Q}_{2}}$
$\Rightarrow {{Q}_{2}}=\dfrac{aQ}{a+b}$.
Similarly,
${{Q}_{1}}=\dfrac{bQ}{a+b}$.
This means that charge on the surface 1 is ${{Q}_{1}}=\dfrac{bQ}{a+b}$.
The charge on surface 2 is $-{{Q}_{1}}=\dfrac{-bQ}{a+b}$.
The charge on surface 3 is ${{Q}_{1}}=\dfrac{bQ}{a+b}$.
The charge on surface 4 is ${{Q}_{2}}=\dfrac{aQ}{a+b}$.
The charge on surface 5 is $-{{Q}_{2}}=\dfrac{-aQ}{a+b}$.
The charge on surface 6 is ${{Q}_{2}}=\dfrac{aQ}{a+b}$.

Note:
Note that the electric field inside a conductor is always zero. The charges are induced on the conductors in such a way that the net electric everywhere inside each conductor is zero.
Also, note that all the charge on the conductor is present on the surface of the conductor only. There is no net charge inside a conductor.