Question

Three houses are available in a locality. Three people apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house, is
A. $\dfrac{7}{9}$
B. $\dfrac{8}{9}$
C. $\dfrac{1}{9}$
D. $\dfrac{2}{9}$

Answer 1

Hint: We will first find the total possible combination of houses to be selected. Then we will find the number of ways three persons can apply for houses and finally we will find the probability that all of them have applied for the same house.

Complete step-by-step answer:
It is given in the question that three houses are available in a locality. Also, three people apply for the houses and each of them apply for one house without consulting others. Then, we have to find the probability that all of them apply for the same houses. Let us consider the representation below.
H1, H2 or H3
So, number of houses = 3
Also, one person can select one house in ${}^{3}{{C}_{1}}$ ways. Here, we can use the formula,
${}^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!}$
Substituting the value of n = 3 and r = 1, we get,
${}^{3}{{C}_{1}}=\dfrac{3!}{1!\left( 3-1 \right)!}$
${}^{3}{{C}_{1}}=\dfrac{3\times 2!}{2!}=3$
Thus, one person can select one house in 3 ways. He has to select one among H1, H2 or H3.
Now, from this we can find the total possible combination - the total possibility that three persons can select one house out of 3. Let us represent it as below. H represents houses and P represents persons.

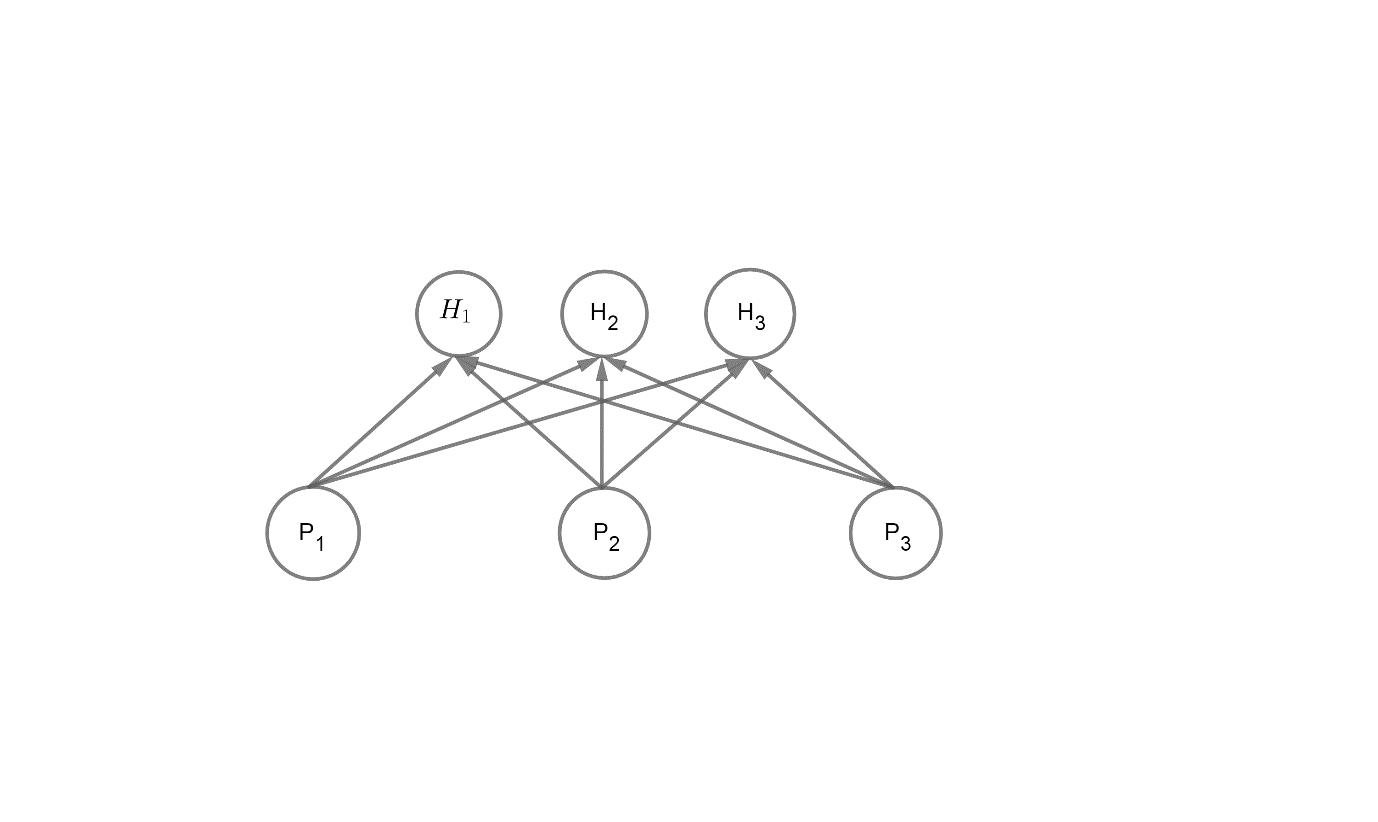
So, from this above picture we get an idea that each and every individual has three choices.
${{P}_{1}}$ may apply for house H1, H2 or H3. Similarly, ${{P}_{2}}$ may apply for house H1, H2 or H3 and ${{P}_{3}}$may apply for house H1, H2 or H3.
\[\underset{\underset{3}{\mathop{\downarrow }}\,}{\mathop{H1}}\,\underset{\underset{3}{\mathop{\downarrow }}\,}{\mathop{H2}}\,\underset{\underset{3}{\mathop{\downarrow }}\,}{\mathop{H3}}\,\]
So, from the above discussion we can conclude that for each house we can have 3 applications. Thus the total possible combination can be represented as $3\times 3\times 3$ or ${{\left( 3 \right)}^{3}}$. Therefore, we can say that the total possibility that all of them applied for one house out of 3 is $3\times 3\times 3={{\left( 3 \right)}^{3}}=27$.
Now, we have all the required data to find probability. So, the probability that all of them applied for the same house $=\dfrac{number\ of\ houses}{total\ possible\ combination\ to\ apply\ for\ house}$.
We have a number of houses = 3 and total possible combinations to apply for houses = 27. So, on putting the value of number of houses as 3 and total possible combination to apply for houses as 27 in obtained formula, we get,
Probability that all of them applied for the same house $=\dfrac{3}{27}$ .
Dividing numerator and denominator by 3, we get;
$\dfrac{3}{27}=\dfrac{1}{9}$
Thus, the probability that all of them have applied for the same house will be $\dfrac{1}{9}$.
Answer is option C.
Note: This question is can be solved in few steps as:
Step 1 - Find the total possible combination of house which is ${}^{3}{{C}_{1}}=3$.
Step 1 –Total possible combination that three person can apply for house = 3 X 3 X 3 = 27
Step 3 – Probability that all of them have applied for the same house $=\dfrac{3}{27}=\dfrac{1}{9}$.
Use the formula ${}^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!}$to make your calculation short and always make a diagram for reference in question.