Question

Three concentric spherical shells have radii a, b and c $\left( a\langle b\langle c \right)$ and have surface charge densities as $+\sigma ,-\sigma ,+\sigma $ respectively. If ${{V}_{A}},{{V}_{B}}\text{ and }{{V}_{C}}$ denote the potentials of three shells, then for $c=a+b$, we have:
$\begin{align}
  & \left( A \right){{V}_{C}}={{V}_{B}}={{V}_{A}} \\
 & \left( B \right){{V}_{C}}={{V}_{B}}\ne {{V}_{A}} \\
 & \left( C \right){{V}_{C}}\ne {{V}_{B}}={{V}_{A}} \\
 & \left( D \right){{V}_{C}}\ne {{V}_{B}}\ne {{V}_{A}} \\
\end{align}$

Answer 1

Hint: We will first of all draw a proper diagram to get a better understanding of our problem. The second step will be to write the surface charge of each shell using their radii and surface charge densities. Now, we will use the formula for potential of an electrically charged shell at its surface which is given by: $V=\dfrac{1}{4\pi \varepsilon }\dfrac{Q}{r}$ . ‘r’ being the radius of shell and ‘Q’ its surface charge. We shall proceed in this manner to get our solution.
Complete step by step solution: Let us first of all draw a proper diagram to understand our problem. This is done as follows:
                       

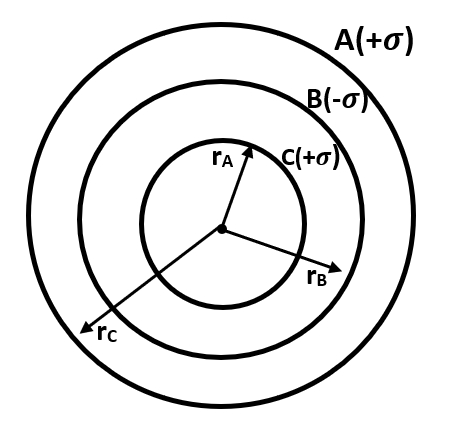
Now the situation is pretty clear to us and thus we can move on to our next step, that is, writing the charges on each sphere. This can be done as follows:
$\begin{align}
  & \Rightarrow {{Q}_{A}}=+\sigma \left( 4\pi {{a}^{2}} \right) \\
 & \Rightarrow {{Q}_{B}}=-\sigma \left( 4\pi {{b}^{2}} \right) \\
 & \Rightarrow {{Q}_{C}}=+\sigma \left( 4\pi {{c}^{2}} \right) \\
\end{align}$
Now that we have the value of charges on all the concentric shells, we can easily calculate the potential of each sphere. This is done as follows:
The potential of shell ‘C’ is due to all the charges present inside. This is equal to:
$\begin{align}
  & \Rightarrow {{V}_{C}}=\dfrac{1}{4\pi \varepsilon }\left( \dfrac{{{Q}_{A}}}{c}+\dfrac{{{Q}_{B}}}{c}+\dfrac{{{Q}_{C}}}{c} \right) \\
 & \Rightarrow {{V}_{C}}=\dfrac{1}{4\pi \varepsilon c}\left( {{Q}_{A}}+{{Q}_{B}}+{{Q}_{C}} \right) \\
 & \Rightarrow {{V}_{C}}=\dfrac{1}{4\pi \varepsilon c}\left[ +\sigma \left( 4\pi {{a}^{2}} \right)-\sigma \left( 4\pi {{b}^{2}} \right)+\sigma \left( 4\pi {{c}^{2}} \right) \right] \\
 & \Rightarrow {{V}_{C}}=\dfrac{\sigma }{4\pi \varepsilon c}\left[ 4\pi \left( {{a}^{2}}-{{b}^{2}}+{{c}^{2}} \right) \right] \\
 & \Rightarrow {{V}_{C}}=\dfrac{\sigma }{\varepsilon }\left( \dfrac{{{a}^{2}}}{c}-\dfrac{{{b}^{2}}}{c}+c \right) \\
\end{align}$
Now, the potential al the surface of shell ‘B’ will be equal to:
$\begin{align}
  & \Rightarrow {{V}_{B}}=\dfrac{1}{4\pi \varepsilon }\left( \dfrac{{{Q}_{A}}}{b}+\dfrac{{{Q}_{B}}}{b}+\dfrac{{{Q}_{C}}}{c} \right) \\
 & \Rightarrow {{V}_{B}}=\dfrac{1}{4\pi \varepsilon }\left( \dfrac{\sigma \left( 4\pi {{a}^{2}} \right)}{b}-\dfrac{\sigma \left( 4\pi {{b}^{2}} \right)}{b}+\dfrac{\sigma \left( 4\pi {{c}^{2}} \right)}{c} \right) \\
 & \Rightarrow {{V}_{B}}=\dfrac{\sigma }{\varepsilon }\left( \dfrac{{{a}^{2}}}{b}-b+c \right) \\
\end{align}$
And, the potential at the surface of shell ‘A’ will be equal to:
$\begin{align}
  & \Rightarrow {{V}_{A}}=\dfrac{1}{4\pi \varepsilon }\left( \dfrac{{{Q}_{A}}}{a}+\dfrac{{{Q}_{B}}}{b}+\dfrac{{{Q}_{C}}}{c} \right) \\
 & \Rightarrow {{V}_{A}}=\dfrac{1}{4\pi \varepsilon }\left( \dfrac{\sigma \left( 4\pi {{a}^{2}} \right)}{a}-\dfrac{\sigma \left( 4\pi {{b}^{2}} \right)}{b}+\dfrac{\sigma \left( 4\pi {{c}^{2}} \right)}{c} \right) \\
 & \Rightarrow {{V}_{A}}=\dfrac{\sigma }{\varepsilon }\left( a-b+c \right) \\
\end{align}$
Putting, $c=a+b$, in the potential expression of all the three shells and simplifying, we get:
$\begin{align}
  & \Rightarrow {{V}_{C}}=\dfrac{2\sigma }{\varepsilon }\left( a \right) \\
 & \Rightarrow {{V}_{B}}=\dfrac{a\sigma }{\varepsilon }\left( \dfrac{2a+b}{a+b} \right) \\
 & \Rightarrow {{V}_{A}}=\dfrac{2\sigma }{\varepsilon }\left( a \right) \\
\end{align}$
From these results we can clearly see that:
$\Rightarrow {{V}_{C}}\ne {{V}_{B}}={{V}_{A}}$

Hence, option (C) is the correct option.

Note:
In problems like these, we should be careful in writing the potential of inner shells as they are comparatively harder. Also, in lengthy calculations like these, be sure to check and verify your calculation at each step of the process as reviewing the solution at each step is better than reviewing the solution at the end.