Question

Three circularly shaped linear polarisers are placed coaxially. The transmission axis of the first polariser is at 30$^\circ $, the second one is at 60$^\circ $ and the third at 90$^\circ $ to the vertical all in the clockwise sense. Each polarizer additionally absorbs 10$\% $ of the light. If a vertically polarised beam of light of intensity $I = 100W/{m^2}$ is incident on this assembly of polarisers, then the final intensity of the transmitted light will be close to:
$\begin{array}{l}
{\rm{A}}{\rm{. 10}}W/{m^2}\\
{\rm{B}}{\rm{. 20}}W/{m^2}\\
{\rm{C}}{\rm{. 30}}W/{m^2}\\
{\rm{D}}{\rm{. 50}}W/{m^2}
\end{array}$

Answer 1

Hint: The intensity of the light obtained after passing through a polariser is given by the Brewster’s law. According to this law, the intensity of light obtained is directly proportional to the square of the cosine of the angle that the polariser axis makes with the transmission axis.

Formula used:
The Brewster law be given as
$I = {I_0}{\cos ^2}\theta $
Here ${I_0}$ is the initial intensity of the light while $I$ is the intensity of light obtained after passing through the polarizer. The angle that the transmission axis of the polarizer makes with the vertical is given as $\theta $.

Detailed step by step solution:
We are given that we have three circularly shaped polarizers which are placed coaxially. The following diagram shows the cross-section of the three polarizers. According to the given information, each polarizer is at an angle of 30$^\circ $ with respect to the previous polarizer.

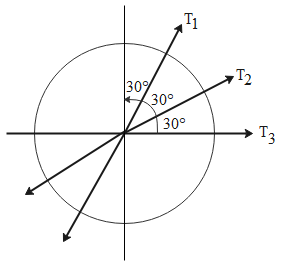
We are also given that the polarizers additionally decrease the intensity of light by absorbing 10$\% $ of the light.
The initial intensity of the light is given as
${I_0} = 100W/{m^2}$
Now we can use the Brewster law given in equation (i) to calculate the intensity of light coming out of the various polarizers.
Let ${I_1}$ is the intensity of light after passing through first polarizer, ${I_2}$ is the intensity of light after passing through second polarizer and ${I_3}$ is the intensity of light after passing through third polarizer. All three polarizers are aligned at an angle of 30\[^\circ \] with respect to one another.
$\begin{array}{l}
{I_1} = {I_0} \times \dfrac{{90}}{{100}} \times {\cos ^2}30^\circ = \dfrac{3}{4} \times \dfrac{9}{{10}}{I_0}\\
{I_2} = {I_1} \times \dfrac{{90}}{{100}} \times {\cos ^2}30^\circ = {\left( {\dfrac{3}{4} \times \dfrac{9}{{10}}} \right)^2}{I_0}\\
{I_3} = {I_2} \times \dfrac{{90}}{{100}} \times {\cos ^2}30^\circ = {\left( {\dfrac{3}{4} \times \dfrac{9}{{10}}} \right)^3}{I_0}\\
\therefore {I_3} = {\left( {\dfrac{3}{4} \times \dfrac{9}{{10}}} \right)^3}{I_0}\\
{I_3} = 30.75W/{m^2}
\end{array}$
Hence, the correct answer must be option C.

Note: It should be noted that the polarizers absorb the 10$\% $ of light additionally which means that they allow only $90\% $ of the light to pass through. This is the reason why we take $90\% $ in the above expressions.