Question

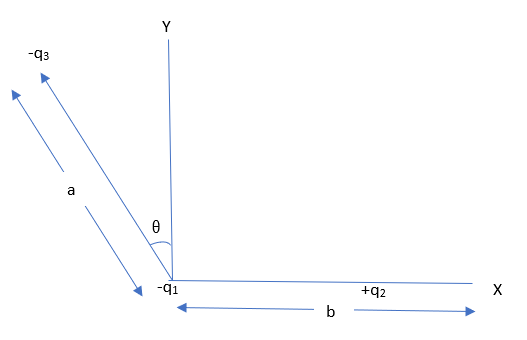
Three charges $ - {q_1} $ , $ + {q_2} $ and $ - {q_3} $ are placed as shown in the figure. The x-component of the force on $ - {q_1} $ is proportional to:
 $
  \left( {\text{A}} \right)\dfrac{{{q_2}}}{{{b^2}}} - \dfrac{{{q_3}}}{{{a^2}}}\cos \theta \\
  \left( {\text{B}} \right)\dfrac{{{q_2}}}{{{b^2}}} + \dfrac{{{q_3}}}{{{a^2}}}\sin \theta \\
  \left( {\text{C}} \right)\dfrac{{{q_2}}}{{{b^2}}} + \dfrac{{{q_3}}}{{{a^2}}}\cos \theta \\
  \left( {\text{D}} \right)\dfrac{{{q_2}}}{{{b^2}}} - \dfrac{{{q_3}}}{{{a^2}}}\sin \theta \\
  $

Answer 1

Hint : Since we have been given three charges, first try to find the forces on charge $ {q_1} $ due to the other two charges since we have to find the x-component of force on $ - {q_1} $ . The force between two charges is to be found out by coulombs formula. After this step find out the x-component of the force.
 $ {\text{F = k}}\dfrac{{{q_1}{q_2}}}{{{r^2}}} $
Where F= electric force
k=Coulomb constant
 $ {q_1},{q_2} $ = charges
r=distance of separation.

Complete Step By Step Answer:
we have been given three charges $ - {q_1} $ , $ + {q_2} $ and $ - {q_3} $ also we have been shown in the diagram about the placements of this charges. All we have to find is the x-component of the force $ - {q_1} $ .
We all know that the charges present in the given position will have repulsive and attractive forces between each other. Hence $ - {q_1} $ and $ - {q_3} $ will repel each other and this two charges will attract $ + {q_2} $ .
hence we will try to calculate the force between these charges. Since we have to find the x-component of force on $ - {q_1} $ , we will try to find the force on $ - {q_1} $ due to $ + {q_2} $ and $ - {q_3} $ .
We will use the formula $ {\text{F = k}}\dfrac{{{q_1}{q_2}}}{{{r^2}}} $
Where F= electric force
k=Coulomb constant
 $ {q_1},{q_2} $ = charges
r=distance of separation.
Hence the force due to $ {q_2} $ on $ {q_1} $ is $ {{\text{F}}_{12}}{\text{ = k}}\dfrac{{{q_1}{q_2}}}{{{b^2}}} $ as the distance between this two charges is b.
The force due to $ {q_3} $ on $ {q_1} $ is $ {{\text{F}}_{13}}{\text{ = k}}\dfrac{{{q_1}{q_3}}}{{{a^2}}} $ as the distance between this two charges is a.
x-component of the force on $ {q_1} $ will be $ {F_{12}} + {F_{13}}\sin \theta $
hence $ {F_x} = {\text{k}}\dfrac{{{q_1}{q_2}}}{{{b^2}}}{\text{ + k}}\dfrac{{{q_1}{q_3}}}{{{a^2}}}\sin \theta $
 $ {F_x} $ $ \alpha \dfrac{{{q_2}}}{{{b^2}}}{\text{ + }}\dfrac{{{q_3}}}{{{a^2}}}\sin \theta $
hence option (B) matches our solution.
Hence (B) $ \dfrac{{{q_2}}}{{{b^2}}}{\text{ + }}\dfrac{{{q_3}}}{{{a^2}}}\sin \theta $ is the right answer.

Note :
While solving problems of this type, you should always draw a diagram indicating the forces on the charge. Also find out the directions of the vector by looking at the sign and draw in it the diagram. Since force is a vector, so when one or more charges exert pressure on the other, the net force on the charge is the vector sum of the individual forces.