Question

Three charges $-q,+q\text{ and }-q$ are kept at the corners of an equilateral triangle having side $a$. The resultant electric force on a charge $+q$ kept at the centroid O of the triangle will be given as,
$\begin{align}
  & A.\dfrac{3{{q}^{2}}}{4\pi {{\varepsilon }_{0}}{{a}^{2}}} \\
 & B.\dfrac{{{q}^{2}}}{4\pi {{\varepsilon }_{0}}{{a}^{2}}} \\
 & C.\dfrac{{{q}^{2}}}{2\pi {{\varepsilon }_{0}}{{a}^{2}}} \\
 & D.\dfrac{3{{q}^{2}}}{2\pi {{\varepsilon }_{0}}{{a}^{2}}} \\
\end{align}$

Answer 1

Hint: An equilateral triangle is having the three sides as well as their angles to be equal. The angle of the equilateral triangle has been given as $60{}^\circ $. Find the cosine of the half of this angle. From this find the perpendicular distance from the centroid to one of the sides of the equilateral triangle. Find the resultant force. This will help you in answering this question.

Complete step by step answer:
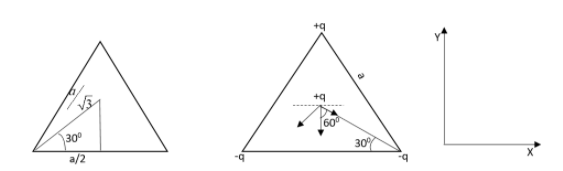
The cosine of the half of the angle has been given as,
\[\cos 30{}^\circ =\dfrac{a}{2x}\]
Rearranging this equation will give,
\[\begin{align}
  & \dfrac{\sqrt{3}}{2}=\dfrac{a}{2x} \\
 & \Rightarrow x=\dfrac{2a}{2\sqrt{3}} \\
 & \Rightarrow x=\dfrac{a}{\sqrt{3}} \\
\end{align}\]
Therefore the perpendicular distance from the centroid to any of the sides has been calculated.
The net force on the x axis is cancelled by the two charges placed below \[-q\]. Therefore the force on the y-axis is added up.
Therefore the force on y-axis can be given as the equation,
\[{{F}_{y}}=\dfrac{k\left( q \right)\left( q \right)}{{{\left( \dfrac{a}{\sqrt{3}} \right)}^{2}}}+\dfrac{k\left( q \right)\left( q \right)}{{{\left( \dfrac{a}{\sqrt{3}} \right)}^{2}}}\times \cos 60{}^\circ \times 2\]
We have to simplify this equation accordingly.
That can be written as,
\[\begin{align}
  & {{F}_{y}}=\dfrac{3k{{\left( q \right)}^{2}}}{{{a}^{2}}}+\dfrac{3k{{\left( q \right)}^{2}}}{{{a}^{2}}} \\
 & \Rightarrow {{F}_{y}}=\dfrac{6k{{\left( q \right)}^{2}}}{{{a}^{2}}} \\
\end{align}\]
As we all know, the constant \[k\] can be shown as an equation given by,
\[k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\]
Let us substitute this in the equation of force on the y-axis. That is we can write that,
\[{{F}_{y}}=\dfrac{6{{\left( q \right)}^{2}}}{4\pi {{\varepsilon }_{0}}{{a}^{2}}}=\dfrac{3{{q}^{2}}}{2\pi {{\varepsilon }_{0}}{{a}^{2}}}\]
Therefore, the answer has been obtained. This has been given as the option D.

Note:
The electrostatic force is otherwise defined as the Coulomb interaction or Coulomb force. It can be explained as the attractive or repulsive force in between two electrically charged bodies. As we all know, the like charges will get repelled each other whereas unlike charges attract each other.