Question

Three capacitors each of capacitance \[9pF\] are connected in series as shown in figure.

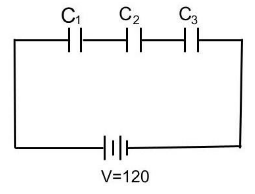
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor, if the combination is connected to a \[120\,volt\] supply?

Answer 1

Hint: To answer the question, we must first determine the capacitance, which we can do by using the formula for determining capacitance when two or more capacitors are connected in series. Summing the reciprocals of the individual capacitances and calculating the reciprocal of the sum can be used to compute the total capacitance of capacitors in series. Then, because the capacitance is equal and connected in series so voltage divides to find voltage across each capacitor.

Complete step by step answer:
It is given to us that three capacitors each of capacitance \[9pF\] are connected in series.Therefore,
${C_1} = {C_2} = {C_3} = 9pF = 9 \times {10^{ - 12}}F $

(a) Since the capacitor are connected in series
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}$
Now, putting the values in ${C_1}$ , ${C_2}$ and ${C_3}$
$\dfrac{1}{C} = \dfrac{1}{{9 \times {{10}^{ - 12}}}} + \dfrac{1}{{9 \times {{10}^{ - 12}}}} + \dfrac{1}{{9 \times {{10}^{ - 12}}}}$
Now, we will take ${10^{ - 12}}$ as common
$\dfrac{1}{C} = \dfrac{1}{{{{10}^{ - 12}}}}\left[ {\dfrac{1}{9} + \dfrac{1}{9} + \dfrac{1}{9}} \right]$
Now we will add up
$\dfrac{1}{C} = \dfrac{1}{{{{10}^{ - 12}}}} \times \dfrac{3}{9} \\
\Rightarrow \dfrac{1}{C} = \dfrac{1}{{{{10}^{ - 12}}}} \times \dfrac{1}{3}$
$\Rightarrow \dfrac{1}{C} = \dfrac{1}{{3 \times {{10}^{ - 12}}}}$
So, from here the value of $C$
$\therefore C = 3 \times {10^{ - 12}} = 3pF$

Hence, total capacitance of the combination is $3pF$.

(b) Potential difference across each capacitor, if the combination is connected to a \[120\,volt\] supply.It is given to us that combination is connected to a \[120\,volt\] supply.
Therefore, $V = {V_1} + {V_2} + {V_3}$
And as the capacitance are equal
 ${V_1} = {V_2} = {V_3} = V'$(Let)
Therefore, $V = 3V'$. Now, from here we will find out the $V'$ by putting the known values
$V' = \dfrac{V}{3}$
Putting the value of $V$ which is given \[120\,volt\]
$\therefore V' = \dfrac{{120}}{3} = 40V\,\,\,\,\,\,\,\,\,\,\left( {\because {C_1} = {C_2} = {C_3}} \right)$

Hence, potential difference across each capacitor is $40V$.

Note: It's important to note that connecting capacitors in series is done to boost the effective circuit voltage handling capability. Capacitors have a breakdown voltage rating that, if exceeded, increases their risk of failure dramatically. The voltage across two identical capacitors will be divided in half.