Question

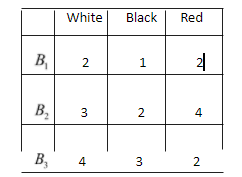
Three boxes${B_1}$,${B_2}$,${B_3}$ contain balls with different colours as follows:

Answer 1

Hint: Here, we are required to find the probability that the ball has been drawn from box ${B_2}$ where it is given that the ball is red in colour. We would use Bayes’ theorem to find the probability (Because it is given that the ball is red in colour and we have to find the probability that it was drawn from${B_2}$).

Formula Used:
$P\left( {A|B} \right) = \dfrac{{P\left( {B|A} \right)P\left( A \right)}}{{P\left( {B|A} \right)P\left( A \right) + P{{\left( {B|A} \right)}^C}P{{\left( A \right)}^C}}}$

Complete step-by-step answer:
According to the question, there are three boxes: ${B_1}$,${B_2}$ and${B_3}$
Also, when a dice is thrown, the total number of possible outcomes is 6.
It is given that, when a dice is thrown:
If 1 or 2 turns up on the dice, box ${B_1}$ is selected;
Hence, probability of box ${B_1} = P\left( {{B_1}} \right) = \dfrac{2}{6}$
(As total probability$ = $Number of favourable outcomes/Total number of outcomes)
Similarly,
If 3 or 4 turns up, ${B_2}$is selected;
Hence, probability of box ${B_2} = P\left( {{B_2}} \right) = \dfrac{2}{6}$
And,
If 5 or 6 turns up, then ${B_3}$ is selected;
Hence, probability of box ${B_3} = P\left( {{B_3}} \right) = \dfrac{2}{6}$
Now, according to the question, a box is selected like this and a ball is drawn from that box.
Also, the ball is red in colour.
Hence, as we know,
For box${B_1}$:
Total number of balls$ = 5$
Number of Red balls$ = 2$
Hence, probability of red ball$ = \dfrac{2}{5}$
Similarly,
For box${B_2}$:
Total number of balls$ = 9$
Number of Red balls$ = 4$
Hence, probability of red ball$ = \dfrac{4}{9}$
Also,
For box${B_3}$:
Total number of balls$ = 9$
Number of Red balls$ = 2$
Hence, probability of red ball$ = \dfrac{2}{9}$
Now, it is given that the ball is red in colour and we have to find the probability that it was drawn from${B_2}$.
Hence, we would use Bayes’ formula, i.e.
$P\left( {A|B} \right) = \dfrac{{P\left( {B|A} \right)P\left( A \right)}}{{P\left( {B|A} \right)P\left( A \right) + P{{\left( {B|A} \right)}^C}P{{\left( A \right)}^C}}}$
According to the Bayes’ theorem, probability of an event B, given that event A has already occurred, is the sum of conditional probabilities of event B.
 We would understand this by applying this theorem in this question.
Now, we are given that the ball is red in colour and we have to find the probability that it was drawn from${B_2}$.
Hence,
Probability that the ball is drawn from box ${B_2}$ knowing that it is red in colour$ = $
Probability of red ball being from ${B_2}$/ Probability of red ball being from ${B_1} + $ Probability of red ball being from ${B_2} + $ Probability of red ball being from ${B_3}$
Hence, required probability$ = \dfrac{{\dfrac{2}{6} \times \dfrac{4}{9}}}{{\dfrac{2}{6} \times \dfrac{2}{5} + \dfrac{2}{6} \times \dfrac{4}{9} + \dfrac{2}{6} \times \dfrac{2}{9}}}$
$ = \dfrac{{\dfrac{4}{{27}}}}{{\dfrac{2}{{15}} + \dfrac{4}{{27}} + \dfrac{2}{{27}}}}$
$ = \dfrac{{\dfrac{4}{{27}}}}{{\dfrac{2}{{15}} + \dfrac{2}{9}}}$
Taking LCM of 15 and 9, and solving the fraction part in the denominator,
$ = \dfrac{{\dfrac{4}{{27}}}}{{\dfrac{{6 + 10}}{{45}}}}$
$ = \dfrac{{\dfrac{4}{{27}}}}{{\dfrac{{16}}{{45}}}}$
This can be written as:
$ = \dfrac{4}{{27}} \times \dfrac{{45}}{{16}}$
Solving further,
$ = \dfrac{1}{3} \times \dfrac{5}{4}$
$ = \dfrac{5}{{12}}$
Therefore, if the ball drawn is red, then the probability that it was drawn from${B_2} = \dfrac{5}{{12}}$
Hence, this is the required answer.

Note: We should know what is given and what is required to be found to answer this question correctly. This is because if there is confusion between the two then there are chances that the Bayes’ theorem is not applied correctly and our answer becomes incorrect. Hence, this distinction is really important to answer the question correctly.