Question

There are five cities A, B, C, D and E on a certain island. Each city is connected to every other city by road. In how many ways can a person starting from city A come back to A after visiting some cities without visiting a city more than once and without taking the same road more than once? (The order in which he visits the cities also matters: e.g., the routes \[A \to B \to C \to A\] and \[A \to C \to B \to A\] are different)

Answer 1

Hint:
Here, we will find the number of ways that a person visits all the four cities, three cities, and two cities by using a combination formula. We will then add all the number of ways, to get the required answer.

Formula Used:
Combination is given by the formula \[{}^n{C_r} = \dfrac{{n!}}{{\left( {n - r} \right)!r!}}\].

Complete step by step solution:
We are given five cities A, B, C, D and E on a certain island. Each city is connected to every other city by road.
So, we can depict the given information in form of a diagram:

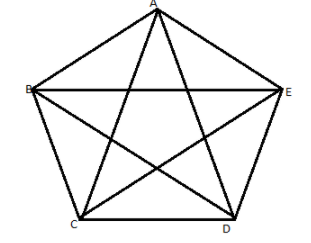
We will consider that a person is visiting all the four cities, so, we get
Number of ways of visiting all the four cities \[ = 4! = 4 \times 3 \times 2 \times 1\]
Multiplying the terms, we get
\[ \Rightarrow \] Number of ways of visiting all the four cities \[ = 24\]
Now, We will consider that a person is visiting three cities, so, we get
 Number of ways of visiting three cities \[ = {}^4{C_3} \cdot 3!\]
Using combination formula \[{}^n{C_r} = \dfrac{{n!}}{{\left( {n - r} \right)!r!}}\], we get
\[ \Rightarrow \] Number of ways of visiting three cities \[ = \dfrac{{4 \times 3 \times 2}}{{1 \times 2 \times 3}} \times 3!\]
Simplifying the expression, we get
\[ \Rightarrow \] Number of ways of visiting three cities \[ = 24\]
Now, We will consider that a person is visiting two cities, so, we get
Number of ways of visiting two cities \[ = {}^4{C_2} \cdot 2!\]
Using combination formula \[{}^n{C_r} = \dfrac{{n!}}{{\left( {n - r} \right)!r!}}\], we get
\[ \Rightarrow \] Number of ways of visiting two cities \[ = \dfrac{{4 \times 3}}{{1 \times 2}} \times 2!\]
Simplifying the expression, we get
\[ \Rightarrow \] Number of ways of visiting two cities \[ = 12\]
It is not possible for a person to visit only one city since a person cannot take a road more than once.
Now, we will find the total number of ways by adding the number of ways of visiting four cities, three cities, and two cities. Therefore,
Total Number of ways of visiting the cities \[ = 24 + 24 + 12\]
Adding the terms, we get
\[ \Rightarrow \] Total Number of ways of visiting the cities \[ = 60\]

Therefore, the total number of required ways is 60.

Note:
We know that there is not much difference between permutation and combination. The permutation is the way of arranging numbers in some order whereas combination is the way of selecting items where order doesn’t matter. Both the word combination and permutation is the way of arrangement. Here, the order matters only in visiting the cities and not in the visiting city which should be at first.