Question

There are 24 identical pillars in a monument. The base diameter and length of each pillar is 126 cm and 4 m respectively. Find the cost of painting all the pillars at the rate of Rs. 75 per ${{m}^{2}}$.

Answer 1

Hint: We first find the radius of the cylindrical shaped pillars. Then using the formula of $2\pi rh$ for lateral surface area, we have the area for one pillar. Here $r,h$ being radius and height respectively. We find the area for 24 pillars. Then we find the total cost.

Complete step-by-step solution:
The base diameter and length of each pillar is 126 cm and 4 m respectively. The radius is half of the diameter which is equal to $\dfrac{126}{2}=63$ cm. Also, $h=4$.

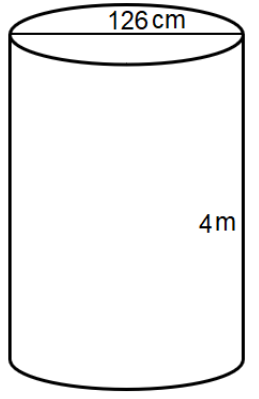
We convert the height into meter form where 63 cm is equal to $r=\dfrac{63}{100}=0.63$ m.
There are 24 identical pillars in a monument. We have to paint all the pillars.
We paint the side area of the pillars. We first find the lateral surface area of one pillar.
For cylindrical shape the formula for lateral surface area is $2\pi rh$.
Putting the values, we get $2\pi rh=2\times \dfrac{22}{7}\times 0.63\times 4$.
Completing the multiplication, we get a lateral surface area of one pillar is $15.84{{m}^{2}}$.
There are 24 identical pillars in a monument. Total area to be painted is
$24\times 15.84=380.16{{m}^{2}}$.
The cost of painting all the pillars at the rate of Rs. 75 per ${{m}^{2}}$ will be
$75\times 380.16=28512$ Rs.
The cost of painting all the pillars at the rate of Rs. 75 per ${{m}^{2}}$ is Rs. 28512.

Note: We have to remember the top and bottom of the pillars can’t be painted because of them being closed. We have to consider them in the cases of total surface area. We will add $2\pi {{r}^{2}}$ to the lateral surface area to find total surface area.