Question

THEOREM 3 (SAS Similarity Criterion) If in two triangles, one pair of corresponding sides are proportional and the included angles are equal then the two triangles are similar.

Answer 1

Hint: We first take two triangles \[\Delta ABC\;,\Delta DEF\;\]and we do the following construction.

Construction:
We take a point X on AB such that \[AX = DE\]
Through X, we draw a segment \[XY\parallel BC\], intersecting AC at Y
Note that \[\Delta AXY\; \sim \Delta ABC\]
Now, we only have to show that \[\Delta AXY\;\] and \[\Delta DEF\] are congruent.

Complete step by step Answer:

We first take two triangles \[\Delta ABC\;,\Delta DEF\;\]

First, we assume that \[AB{\text{ }} > {\text{ }}DE\].

Given:

\[\dfrac{{DE}}{{AB}} = \dfrac{{DF}}{{AC}}\]

\[\angle D = \angle A\]

To prove: \[\Delta DEF\] is similar to \[\Delta ABC\]

Construction:

We take a point X on AB such that \[AX = DE\]
Through X, we draw a segment \[XY\parallel BC\], intersecting AC at Y

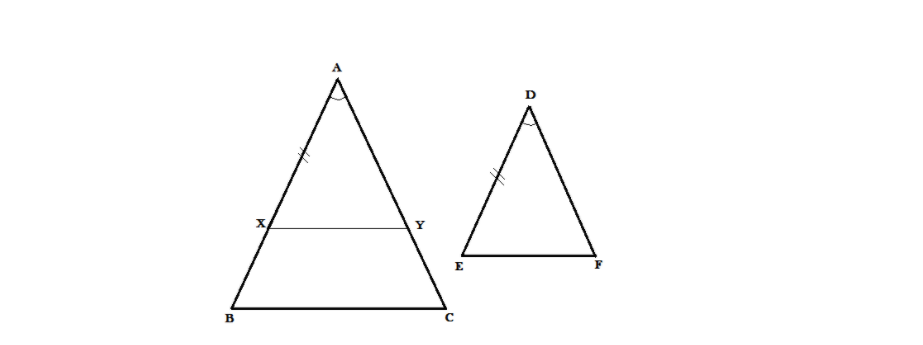
Proof: Since\[XY\parallel BC\], we can see that \[\Delta AXY\; \sim \Delta ABC\]

Therefore,
\[\dfrac{{AX}}{{AB}} = \dfrac{{AY}}{{AC}}\] .... (1) [Since in similar triangles, each pair of corresponding sides are proportional]
Now, we have to show that \[\Delta AXY\;\] and \[\Delta DEF\] are congruent.
It is given that:
\[\dfrac{{DE}}{{AB}} = \dfrac{{DF}}{{AC}}\].... (2)
Since AX = DE (by construction) and from (1) and (2), we have:
\[\dfrac{{DE}}{{AB}} = \dfrac{{AX}}{{AB}} = \dfrac{{AY}}{{AC}} = \dfrac{{DF}}{{AC}}\]
Thus,
\[AY = DF\]
Also, \[AX = DE\] by construction.
And \[\angle D = \angle A\] , given.
Therefore, by the SAS Congruency Criterion,
\[\Delta AXY \cong \Delta DEF\]
$\Rightarrow$\[\Delta AXY \sim \Delta DEF\], since we know that if two triangles are congruent, therefore they are similar.
Now, we already have \[\Delta AXY \sim \Delta ABC\] ,
This implies that,
\[\Delta ABC\] and \[\Delta DEF\;\] are similar.
Hence, proved.

Note: Note that in similar triangles, each pair of corresponding sides are proportional.
Also, if two triangles are congruent, therefore they are similar (although the converse is not always true). Similar triangles are easy to identify because you can apply three theorems specific to triangles. These three theorems, known as Angle - Angle (AA), Side - Angle - Side (SAS), and Side - Side - Side (SSS), are foolproof methods for determining similarity in triangles.