
The $x$- coordinate of the incenter of the triangle that has the coordinate of mid points of its sides are $(0,1),(1,1)$ and $(1,0)$ is
(A) $2 - \sqrt 2 $
(B) $1 + \sqrt 2 $
(C) $1 - \sqrt 2 $
(D) $2 + \sqrt 2 $
Answer
560.1k+ views
Hint: The incenter of a triangle is the center of its inscribed circle. Here, the mid points of the sides of the triangle are given. In order to find the incenter of any triangle, we need the coordinates of the triangle and the length of the corresponding sides respectively. So, we need to find the coordinates of the triangle and the length of its sides. The formula of incenter of any triangle is given below:
$x$- coordinate of the incenter of the triangle= $\dfrac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}}$
Similarly, $y$- coordinate of the incenter of the triangle= $\dfrac{{a{y_1} + b{y_2} + c{y_3}}}{{a + b + c}}$
Where, $a,b$ and $c$ are the length of sides opposite to the coordinates $A({x_1},{y_1}),B({x_2},{y_2})$and $C({x_3},{y_3})$
Complete solution step by step:
After plotting the points given in the question, we get a triangle with coordinates $(0,1), (1,1)$ and $(1,0)$.
$(0,1)$ lies on the $y - $axis and is the midpoint of the first side. Extending $1$ unit above and below $y - $ axis from ($0,1)$, we can get two coordinates of the triangle.
Similarly, $(1,0)$ lies on the $x - $ axis and is the midpoint of the second side. Extending $1$ unit left and right on the $x - $ axis from ($0,1)$, we can get the other coordinate.
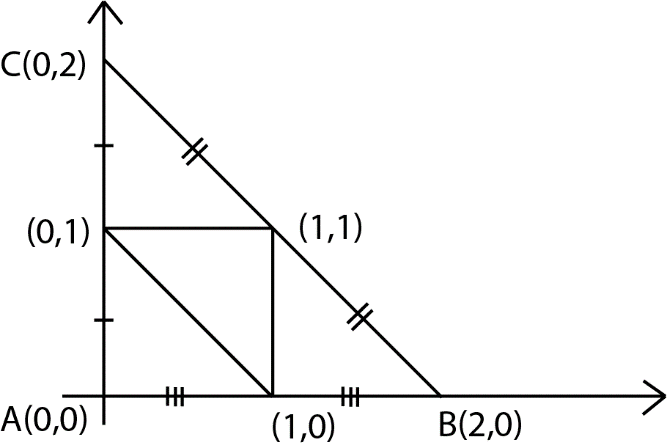
From $\vartriangle ABC$,
We got the coordinates $A(0,0),B(2,0)$and $C(0,2)$.
Distance between any two points $A({x_1},{y_1})$and $B({x_2},{y_2})$=$\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $
$\therefore $length of side $AB$= $\sqrt {{{(0 - 2)}^2} + {{(0 - 0)}^2}} = 2$
Length of side $BC = \sqrt {{{(2 - 0)}^2} + {{(0 - 2)}^2}} = \sqrt {4 + 4} = 2\sqrt 2 $
Length of side $AC = \sqrt {{{(0 - 2)}^2} + {{(0 - 0)}^2}} = 2$
Now, we got all the coordinates and the length of all the sides of the triangle.
We have the formula of incenter:
$x$- coordinate of the incenter of the triangle= $\dfrac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}}$
Where, $a,b$and $c$are the length of sides opposite to the coordinates $A({x_1},{y_1}),B({x_2},{y_2})$and $C({x_3},{y_3})$
Here, $a = BC = 2\sqrt 2 $
$b = AC = 2$
$c = AB = 2$
$A({x_1},{y_1}) = A(0,0)$
$B({x_2},{y_2}) = B(2,0)$
$C({x_3},{y_3}) = C(0,2)$
Putting all the values in the formula,
$x$- coordinate of the incenter of the triangle= $\dfrac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}}$
$ \Rightarrow $$x$- coordinate of the incenter of the triangle = $\dfrac{{2\sqrt 2 \times 0 + 2 \times 2 + 2 \times 0}}{{2\sqrt 2 + 2 + 2}} = \dfrac{4}{{4 + 2\sqrt 2 }} = \dfrac{2}{{2 + \sqrt 2 }}$
On rationalizing $\dfrac{2}{{2 + \sqrt 2 }}$,
$\dfrac{2}{{2 + \sqrt 2 }} = \dfrac{{2(2 - \sqrt 2 )}}{{(2 + \sqrt 2 )(2 - \sqrt 2 )}} = \dfrac{{2(2 - \sqrt 2 )}}{{{2^2} - {{(\sqrt 2 )}^2}}} = 2 - \sqrt 2 $
$ \Rightarrow $$x$- coordinate of the incenter of the triangle = $2 - \sqrt 2 $
Therefore, the correct answer is option (A).
Note:
In this question, we were asked to find the $x - $coordinate of the incenter. But we can find $y - $coordinate also using the formula mentioned in the hint. Substitute the values of $a,b,c$ and the coordinates properly.
$x$- coordinate of the incenter of the triangle= $\dfrac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}}$
Similarly, $y$- coordinate of the incenter of the triangle= $\dfrac{{a{y_1} + b{y_2} + c{y_3}}}{{a + b + c}}$
Where, $a,b$ and $c$ are the length of sides opposite to the coordinates $A({x_1},{y_1}),B({x_2},{y_2})$and $C({x_3},{y_3})$
Complete solution step by step:
After plotting the points given in the question, we get a triangle with coordinates $(0,1), (1,1)$ and $(1,0)$.
$(0,1)$ lies on the $y - $axis and is the midpoint of the first side. Extending $1$ unit above and below $y - $ axis from ($0,1)$, we can get two coordinates of the triangle.
Similarly, $(1,0)$ lies on the $x - $ axis and is the midpoint of the second side. Extending $1$ unit left and right on the $x - $ axis from ($0,1)$, we can get the other coordinate.

From $\vartriangle ABC$,
We got the coordinates $A(0,0),B(2,0)$and $C(0,2)$.
Distance between any two points $A({x_1},{y_1})$and $B({x_2},{y_2})$=$\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $
$\therefore $length of side $AB$= $\sqrt {{{(0 - 2)}^2} + {{(0 - 0)}^2}} = 2$
Length of side $BC = \sqrt {{{(2 - 0)}^2} + {{(0 - 2)}^2}} = \sqrt {4 + 4} = 2\sqrt 2 $
Length of side $AC = \sqrt {{{(0 - 2)}^2} + {{(0 - 0)}^2}} = 2$
Now, we got all the coordinates and the length of all the sides of the triangle.
We have the formula of incenter:
$x$- coordinate of the incenter of the triangle= $\dfrac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}}$
Where, $a,b$and $c$are the length of sides opposite to the coordinates $A({x_1},{y_1}),B({x_2},{y_2})$and $C({x_3},{y_3})$
Here, $a = BC = 2\sqrt 2 $
$b = AC = 2$
$c = AB = 2$
$A({x_1},{y_1}) = A(0,0)$
$B({x_2},{y_2}) = B(2,0)$
$C({x_3},{y_3}) = C(0,2)$
Putting all the values in the formula,
$x$- coordinate of the incenter of the triangle= $\dfrac{{a{x_1} + b{x_2} + c{x_3}}}{{a + b + c}}$
$ \Rightarrow $$x$- coordinate of the incenter of the triangle = $\dfrac{{2\sqrt 2 \times 0 + 2 \times 2 + 2 \times 0}}{{2\sqrt 2 + 2 + 2}} = \dfrac{4}{{4 + 2\sqrt 2 }} = \dfrac{2}{{2 + \sqrt 2 }}$
On rationalizing $\dfrac{2}{{2 + \sqrt 2 }}$,
$\dfrac{2}{{2 + \sqrt 2 }} = \dfrac{{2(2 - \sqrt 2 )}}{{(2 + \sqrt 2 )(2 - \sqrt 2 )}} = \dfrac{{2(2 - \sqrt 2 )}}{{{2^2} - {{(\sqrt 2 )}^2}}} = 2 - \sqrt 2 $
$ \Rightarrow $$x$- coordinate of the incenter of the triangle = $2 - \sqrt 2 $
Therefore, the correct answer is option (A).
Note:
In this question, we were asked to find the $x - $coordinate of the incenter. But we can find $y - $coordinate also using the formula mentioned in the hint. Substitute the values of $a,b,c$ and the coordinates properly.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

Write a letter to the editor of the national daily class 7 english CBSE

Fill in the blanks with appropriate modals a Drivers class 7 english CBSE

What were the major teachings of Baba Guru Nanak class 7 social science CBSE

What are the controls affecting the climate of Ind class 7 social science CBSE





