Question

The volume of this HCP unit cell is:
A. $\text{24}\sqrt{2}{{r}^{3}}$
B. $\text{16}\sqrt{2}{{r}^{3}}$
C. $\text{12}\sqrt{2}{{r}^{3}}$
D. $\dfrac{64}{3\sqrt{3}{{r}^{3}}}$

Answer 1

Hint: Unit cell is the smallest part of the lattice that can describe the entire lattice. In HCP or Hexagonal Close Packing, the arrangement of the spheres is done in such a way that each sphere is in contact with six other spheres.

Complete answer:
-The HCP or Hexagonal Close Packing shows ABABAB…. type of cell packing.
-The given below structure show the HCP packing:

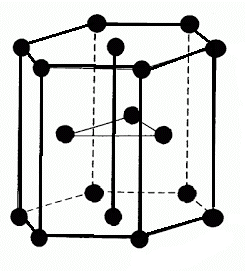
-So, to calculate the volume of HCP, firstly we have to calculate the relation between volume and radius of HCP i.e. \[\text{a = }\dfrac{4\text{r}}{\sqrt{2}}\].
-Here, a is the volume of the unit cell and r is the radius of the atom that is present in the HCP.
-Suppose 'r' is the radius of each atom. So, the volume of the unit cell will be the product of the base area and height (C).
-The base area of a regular hexagon is equal to the area of six equilateral triangles each with side 2r and altitude \[2\text{rSin60}{}^\circ \text{ }\].
-So, Base area = \[\text{6 }\cdot \text{ }\left( \dfrac{1}{2}\text{ }\cdot \text{ 2r}\cdot \text{ }2\text{rSin60}{}^\circ \right)\]
\[=6\text{ }\cdot \text{ }\sqrt{3}{{\text{r}}^{2}}\text{ (as Sin60}{}^\circ \text{ = }\sqrt{3}/2)\]
-Now, we will calculate the height, C
C = \[\text{2 }\cdot \text{ (1/3 of body diagonal of FCC)}\]
= \[\text{2 }\cdot \text{ }\dfrac{1}{3}\sqrt{3}\text{a = }\dfrac{2\text{a}}{\sqrt{3}}\text{ = 4r}\sqrt{\dfrac{2}{3}}\]
-So, the volume of the unit cell will be:
\[\text{6}\sqrt{3}{{\text{r}}^{2}}\text{ }\cdot \text{ 4r}\sqrt{\dfrac{2}{3}}\text{ = 24}\sqrt{2}{{\text{r}}^{3}}\]

Therefore, option A is the correct answer.

Note:
We can also calculate the efficiency of the packaging of the cell by using the formula of packaging i.e the ratio of the volume of the sphere by volume of the cube and then the result is multiplied by 100. The packaging efficiency for CCP is 74% and for BCC, it is 68%.