Question

The volume of a right circular cylinder is 748 $c{m^3}$ and its length is 14cm and external radius is 9cm. Find its thickness.

Answer 1

Hint: By using the formula for volume of cylinder with given inner radius and outer radius, find out the inner radius of cylinder. After that, subtract inner radius from outer radius to get the thickness of the cylinder.

Complete step-by-step answer:
Let r be the inner radius of the cylinder, R be the outer radius of the cylinder and h be the height of the cylinder.

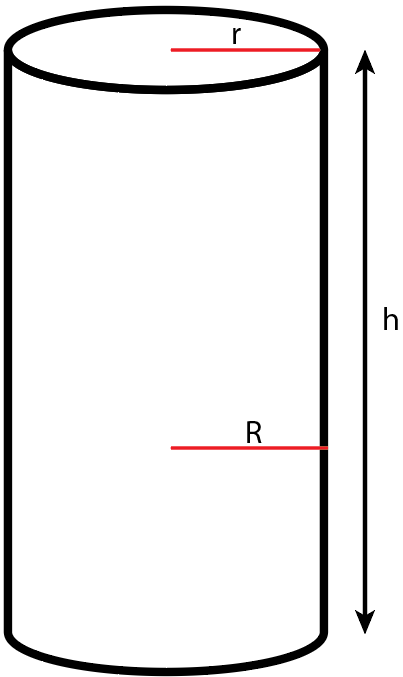
It is given that,
 \[
  R = 9cm \\
  h = 14cm \\
 \]
The volume of the cylinder is given by \[V = \pi \left( {{R^2} - {r^2}} \right)h\]
 \[
  \Rightarrow 748 = \pi \left( {{9^2} - {r^2}} \right) \times 14 \\
  \Rightarrow \dfrac{{748}}{{14\pi }} = 81 - {r^2} \\
  \Rightarrow 17 = 81 - {r^2} \\
  \Rightarrow {r^2} = 81 - 17 \\
  \Rightarrow {r^2} = 64 \\
  \Rightarrow r = \pm 8 \\
 \]
\[\Rightarrow r = 8\] (Refer note)
We got the inner radius of the cylinder as 8cm.
Now for thickness t, we have to subtract inner radius from outer radius of the cylinder.
 \[
  \Rightarrow t = R - r \\
  \Rightarrow t = 9 - 8 \\
 \]
 \[\Rightarrow t = 1\] cm
Thus, we get the thickness of the cylinder as 1cm.

Note: Radius of any object cannot be negative; thus, we took \[r = 8\]cm.
The volume of the cylinder with thickness ‘t’ can be written as $V = \pi {t^2}h$ .
The thickness of the cylinder can be found by subtracting the inner radius ’r’ of cylinder from the outer radius ‘R’ of cylinder. So, the formula becomes $V = \pi {\left( {R - r} \right)^2}h$