Question

The voltage shown in the figure below is known as a triangular waveform. Determine its rms value.

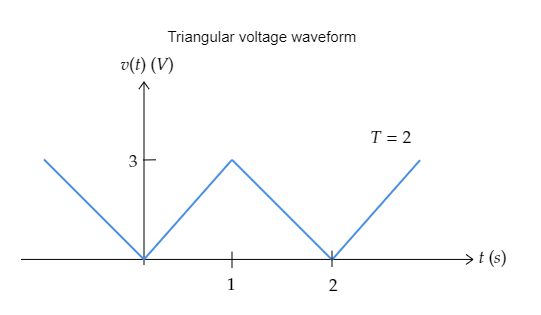
Answer 1

Hint:The rms value refers to the effective value of a varying voltage or a varying current. Here we have to determine the rms voltage of the given triangular form. The rms value of any waveform refers to the root of the area under the squared waveform over the period of the waveform. For a sawtooth or triangular waveform, the rms value of the voltage is also given to be $0 \cdot 577$ or $\dfrac{1}{{\sqrt 3 }}$ times the maximum voltage.

Formulas used:
-The rms voltage of a triangular waveform is given by, ${V_{rms}} = \dfrac{{{V_m}}}{{\sqrt 3 }}$ where ${V_m}$ is the maximum voltage of the varying voltage waveform.
-The rms voltage of any waveform is given by, ${v_{rms}} = \sqrt {\dfrac{A}{T}} $ where $A$ is the area under the squared waveform and $T$ is the period of the waveform.
-The area of a parabola is given by, $A = \dfrac{1}{3}bh$ where $b$ is the horizontal distance to the highest vertical point of the parabola and $h$ is vertical distance to the highest point of the parabola.

Complete step by step answer.
Step 1: Sketch the given triangular waveform and list its important parameters.

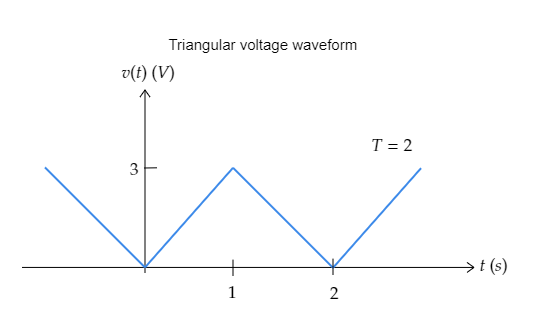
As seen from the above figure, the maximum voltage of the waveform is ${V_m} = 3{\text{V}}$ .
The period of the waveform is mentioned to be $T = 2{\text{s}}$ .
Step 2: Sketch the squared waveform of the given triangular wave and obtain its area.

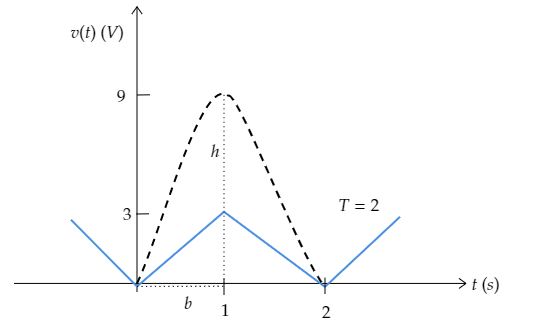
The vertical distance to the highest point in the square waveform will be the square of the maximum voltage of the triangular wave i.e., $h = {V_m}^2 = {3^2}{\text{ = 9V}}$.
The horizontal distance to the highest vertical point on the waveform is observed to be $b = 1{\text{s}}$ .
This squared waveform is a parabola.
The area of a parabola is given by, $A = \dfrac{1}{3}bh$ where $b$ is the horizontal distance to the highest vertical point of the parabola and $h$ is vertical distance to the highest point of the parabola.
From the figure, the area of the squared waveform will be
 $A = \left( {\dfrac{1}{3}bh} \right) + \left( {\dfrac{1}{3}bh} \right) = \dfrac{2}{3}bh$ -------- (1)
Substituting $h = {\text{9V}}$ and $b = 1{\text{s}}$ in equation (2)
$ \Rightarrow A = \dfrac{2}{3} \times 9 \times 1 = 6$
Thus we have the area as $A = 6$ .
Step 3: Express the relation for the rms value of the voltage for a triangular voltage waveform.
Now the rms value of the triangular waveform is defined by, ${v_{rms}} = \sqrt {\dfrac{A}{T}} $ -------- (2)
Substituting for $A = 6$ and $T = 2{\text{s}}$ in equation (2) we get, ${v_{rms}} = \sqrt {\dfrac{6}{2}} = \sqrt 3 {\text{V}}$
Thus the rms value of the voltage is ${v_{rms}} = \sqrt 3 {\text{V}}$ .

Note: Alternate method
For a triangular voltage waveform, the rms value is given by, ${V_{rms}} = \dfrac{{{V_m}}}{{\sqrt 3 }}$ ------ (A)
Substituting in equation (A) we get, ${V_{rms}} = \dfrac{3}{{\sqrt 3 }} = \sqrt 3 {\text{V}}$
Thus the rms value of the triangular voltage waveform is ${V_{rms}} = \sqrt 3 {\text{V}}$ .