Question

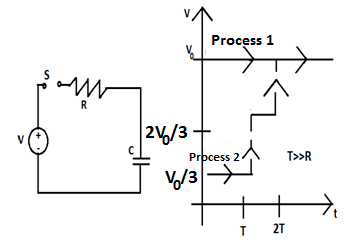
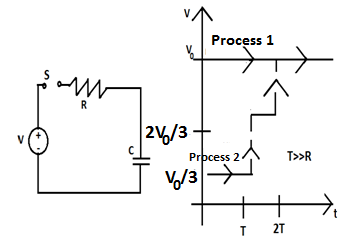
The voltage is set to \[\dfrac{{{V}_{0}}}{3}\] and maintained for a charging time \[T>>RC\]. Then the voltage is raised to \[\dfrac{2{{V}_{0}}}{3}\]without discharging the capacitor and again maintained for a time \[T>>RC\]. The process is repeated one more time by raising the voltage to \[{{V}_{0}}\]and the capacitor is charged to the same final voltage \[{{V}_{0}}\]. In process 2, the total energy dissipated across the resistance \[{{E}_{D}}\]is-
(A). \[{{E}_{D}}=3\left( \dfrac{1}{2}C{{V}_{0}}^{2} \right)\]
 (B). \[{{E}_{D}}=\dfrac{1}{2}C{{V}_{0}}^{2}\]
(C). \[{{E}_{D}}=3C{{V}_{0}}^{2}\]
(D). \[{{E}_{D}}=\dfrac{1}{3}\left( \dfrac{1}{2}C{{V}_{0}}^{2} \right)\]

Answer 1

Hint: When a capacitor is being charged some energy is dissipated across the resistance. The energy stored in a capacitor is directly proportional to the square of the potential difference. The total energy dissipated is the difference of work done by the battery and the energy stored on the capacitor.
Formulas Used:
\[E=\dfrac{1}{2}C{{V}^{2}}\]
\[{{E}_{D}}={{W}_{battery}}-U\]

Complete answer:

A capacitor is a device which stores charge on it in the presence of an electric field. The capacitance is given in farad. The energy stored in a capacitor is given by-
\[E=\dfrac{1}{2}C{{V}^{2}}\]
 Here, \[E\] is the energy stored in a capacitor
\[C\] is it capacitance
\[V\] is the potential difference between the plates of a capacitor
When the battery does work, some of it is stored as energy in the capacitor and some of it is dissipated as heat across the resistor. In the above case, when energy of the capacitance changes due to change in its potential difference, energy is dissipated across the resistor.
Energy dissipated,\[{{E}_{D}}\] is given by-
\[{{E}_{D}}={{W}_{battery}}-U\]
Here,
\[{{W}_{battery}}\] is the work done by the battery
\[U\]is the energy stored in the capacitor
\[\therefore {{E}_{D}}=\dfrac{1}{2}C{{V}_{f}}^{2}-\dfrac{1}{2}C{{V}_{i}}^{2}\]
 \[{{V}_{f}}\,and\,{{V}_{i}}\]are the final and initial potential drops on the capacitor respectively. Therefore, according to process 2-
\[\begin{align}
  & {{E}_{D}}=\dfrac{1}{2}C\left[ {{\left( \dfrac{{{V}_{0}}}{3}-0 \right)}^{2}}+{{\left( \dfrac{2{{V}_{0}}}{3}-\dfrac{{{V}_{0}}}{3} \right)}^{2}}+{{\left( {{V}_{0}}-\dfrac{2{{V}_{0}}}{3} \right)}^{2}} \right] \\
 & \Rightarrow {{E}_{D}}=\dfrac{1}{2}C\left[ \dfrac{{{V}_{0}}^{2}}{9}+\dfrac{{{V}_{0}}^{2}}{9}+\dfrac{{{V}_{0}}^{2}}{9} \right] \\
 & {{E}_{D}}=\dfrac{1}{2}C\left( \dfrac{1}{3}{{V}_{0}}^{2} \right) \\
 & \therefore {{E}_{D}}=\dfrac{1}{3}\left( \dfrac{1}{2}C{{V}_{0}}^{2} \right) \\
\end{align}\]
Therefore, the total energy dissipated across the resistance is \[\dfrac{1}{3}\left( \dfrac{1}{2}C{{V}_{0}}^{2} \right)\].

So, the correct option is (D).

Note:
The potential difference between two points in a circuit is the work done to carry a unit charge from one point to the other. All the energy dissipated in a circuit is dissipated as heat. At \[t=0\] the capacitor is said to be uncharged. The capacitor gets fully charged in time,\[t=\infty \]. After the capacitor is fully charged, the circuit breaks.