Question

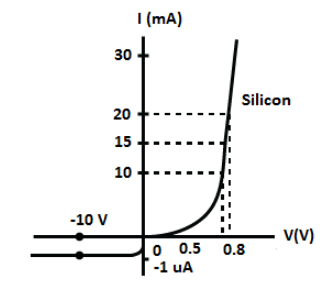
The V-I characteristics of a silicon diode is shown in the figure. Calculate the resistance of the diode at
(a) \[{I_D} = 15\,{\text{mA}}\] and
(b) \[{V_D} = - 10\,{\text{V}}\]

Answer 1

Hint:The inverse of the slope of curve in the V-I graph is the resistance of the diode. Use Ohm’s law to express the resistance of the diode and find the relation between resistance and slope of the curve. For the second part, the change in current is \[ - 1\,\mu A\].

Formula used:
According to Ohm’s law the resistance of the diode is given as,
\[R = \dfrac{{\Delta V}}{{\Delta I}}\]
Here, \[\Delta V\] is the potential across the diode and \[\Delta I\] is the change in the current.

Complete step by step answer:
We have from Ohm’s law the resistance of the diode is given as,
\[R = \dfrac{{\Delta V}}{{\Delta I}}\]
Here, \[\Delta V\] is the potential across the diode and \[\Delta I\] is the change in the current.
Therefore, if we look at the V-I graph of the diode, the resistance is the reciprocal of the slope of the curve. Thus, we can write,
\[R = \dfrac{1}{m} = \dfrac{{{V_2} - {V_1}}}{{{I_2} - {I_1}}}\]
Here, m is the slope of the curve.
(a) At \[{I_D} = 15\,{\text{mA}}\], let’s find the resistance of the diode as follows,
\[R = \dfrac{{{V_2} - {V_1}}}{{{I_2} - {I_1}}}\]
Substituting 0.8 for \[{V_2}\], 0.7 for \[{V_1}\], 20 A for \[{I_2}\] and 10 A for \[{I_1}\] in the above equation, we get,
\[R = \dfrac{{0.8 - 0.7}}{{\left( {20 - 10} \right) \times {{10}^{ - 3}}}}\]
\[ \therefore R = 10\,\Omega \]
Therefore, the resistance of the diode is \[10\,\Omega \].
(b) At \[{V_D} = - 10\,{\text{V}}\], let’s find the resistance of the diode as follows,
\[R = \dfrac{{{V_2} - {V_1}}}{{{I_2} - {I_1}}}\]
Substituting \[ - 10\,{\text{V}}\] for \[{V_2}\], 0 V for \[{V_1}\], \[ - 1\,\mu A\] for \[{I_2}\] and 0 A for \[{I_1}\] in the above equation, we get,
\[R = \dfrac{{ - 10 - 0}}{{\left( { - 1 - 0} \right) \times {{10}^{ - 6}}}}\]
\[ \therefore R = {10^5}\,\Omega \]

Therefore, the resistance of the diode at \[{V_D} = - 10\,{\text{V}}\] is\[{10^5}\,\Omega \].

Note: In I-V characteristics graph, always denote the voltage along the x-axis and current along the y-axis. The reciprocal of the slope is the resistance of the diode and not the slope of the curve. Note that the resistance of the diode is always the positive quantity.