Question

The vertices B and C of a $\Delta ABC$ lie on the line, $\dfrac{x+2}{3}=\dfrac{y-1}{0}=\dfrac{z}{4}$ such that $BC=5$ units. Then the area (in sq. units) of this triangle, given that the point $A\left( 1,-1,2 \right)$ is:\[\]
A.$2\sqrt{34}$\[\]
B. $\sqrt{34}$\[\]
C. $6$\[\]
D. $5\sqrt{17}$\[\]

Answer 1

Hint: We draw the perpendicular AD on BC . We take $\dfrac{x+2}{3}=\dfrac{y-1}{0}=\dfrac{z}{4}=k$ and find any point like D on the line BC as $\left( 3k-2,1,4k \right)$. We find the direction ratios of BC and AD use the relationship between the direction ratios of two lines${{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0$. We obtain $k$ and find the length of AD. We find the area of $\Delta ABC$ as $\dfrac{1}{2}\times BC\times AD$. \[\]

Complete step by step answer:

We know that the direction ratios are any three numbers which are proportional to direction cosines. The direction ratios of any line with a point $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and direction ratios $\left( a,b,c \right)$ is given by
\[\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{z-{{z}_{1}}}{c}\]
We also know that the direction ratios of two perpendicular lines denoted as $\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)$ and $\left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right)$ are related to each other as
${{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0$\[\]
The direction ratios of the line joining two points say $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is $\left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} \right)$\[\]

The given equation of line is
\[\dfrac{x+2}{3}=\dfrac{y-1}{0}=\dfrac{z}{4}....(1)\]
The direction ratios of the above line is $\left( 3,0,4 \right)$. We have from the question that the vertices B and C of $\Delta ABC$ lie on the line. So direction ratios of BC is $\left( 3,0,4 \right)$. The other vertex A has co-ordinate $A\left( 1,-1,2 \right)$ . We draw perpendicular AD on BC.
Let us take $\dfrac{x+2}{3}=\dfrac{y-1}{0}=\dfrac{z}{4}=k$ , where $k$ is any real number. Then we have,
\[\begin{align}
  & \dfrac{x+2}{3}=\dfrac{y-1}{0}=\dfrac{z}{4}=k \\
 & \Rightarrow x=3k-2,y=1,z=4k \\
\end{align}\]
So any point on the line(1) can be expressed as $\left( 3k-2,1,4k \right)$. One such point is $D\left( 3k-2,1,4k \right)$. \[\]

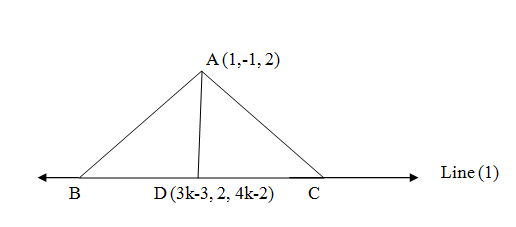
Now we can find the direction ratio of line joining $A\left( 1,-1,2 \right)$ to $D\left( 3k-2,1,4k \right)$ that is AD as $\left( k-2-1,1-\left( 1 \right),4k-2 \right)=\left( 3k-3,2,4k-2 \right)$. Now we have the perpendicular lines AD and BC. So their direction ratios are related as
\[\begin{align}
  & \left( 3k-3 \right)3+\left( 2 \right)0+\left( 4k-2 \right)4=0 \\
 & \Rightarrow 25k=17 \\
 & \Rightarrow k=\dfrac{17}{25} \\
\end{align}\]
So the coordinates of D is $\left( 3\times \dfrac{17}{25}-2,1,4\times \dfrac{17}{25} \right)=\left( \dfrac{1}{25},1,\dfrac{68}{25} \right)$. Now using distance formula between two points we find the length of AD. So we get,
\[AD=\sqrt{{{\left( 1-\dfrac{1}{25} \right)}^{2}}+{{\left( -1-1 \right)}^{2}}+{{\left( 2-\dfrac{68}{25} \right)}^{2}}}=\sqrt{\dfrac{576}{625}+4+\dfrac{324}{625}}=\dfrac{2}{5}\sqrt{34}\]


Now we find the area of the triangle ABC using the formula area $=\dfrac{1}{2}\times $ base$\times $perpendicular. Here the base is BC and perpendicular is AD. So we have been given that $BC=5$ units and we obtained $AD=\dfrac{2}{5}\sqrt{34}$ units. So the area of the triangle is
\[\begin{align}
  & \text{Area}=\dfrac{1}{2}\times BC\times AD \\
 & =\dfrac{1}{2}\times 5\times \dfrac{2}{5}\sqrt{34} \\
 & =\sqrt{34} \\
\end{align}\]
So we have found the area of $\Delta ABC$ as $\sqrt{34}$ square units and the correct option is B.

Note:
  We can alternatively solve by treating BC as vector say $\vec{b}$ and AD as $\vec{a}$ ,then taking half of the cross product $\vec{a}\times \vec{b}$. The acute angle between two lines with direction ratios $\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)$ and $\left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right)$ is $ {{\cos }^{-1}}\left| {{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}} \right| $.