Question

The vertical section of a road over a canal bridge in the direction of its length is in the form of a circle of radius 8.9 metre. Then the greatest speed at which the car can cross this bridge without losing contact with the road at its highest point, the centre of gravity of the car being at a height h = 1.1 metre from the ground. Take g = 10 m/$s^2$.
(A) 5 m/sec
(B) 10 m/sec
(C) 15 m/sec
(D) 20 m/sec

Answer 1

Hint: When a body takes a turn along a closed curve then a centrifugal force acts on in and it which keeps the body going on a closed curve which is then balanced by a centrifugal force which opposite to the centripetal force.

Complete step by step solution:
Given:
The radius of the circle is $R = 8.9\,{\rm{m}}$.
The C.G of car from the ground is $h = 1.1\,{\rm{m}}$.
Let the greatest speed of the vehicle is $V$.
Refer to the free body diagram below.

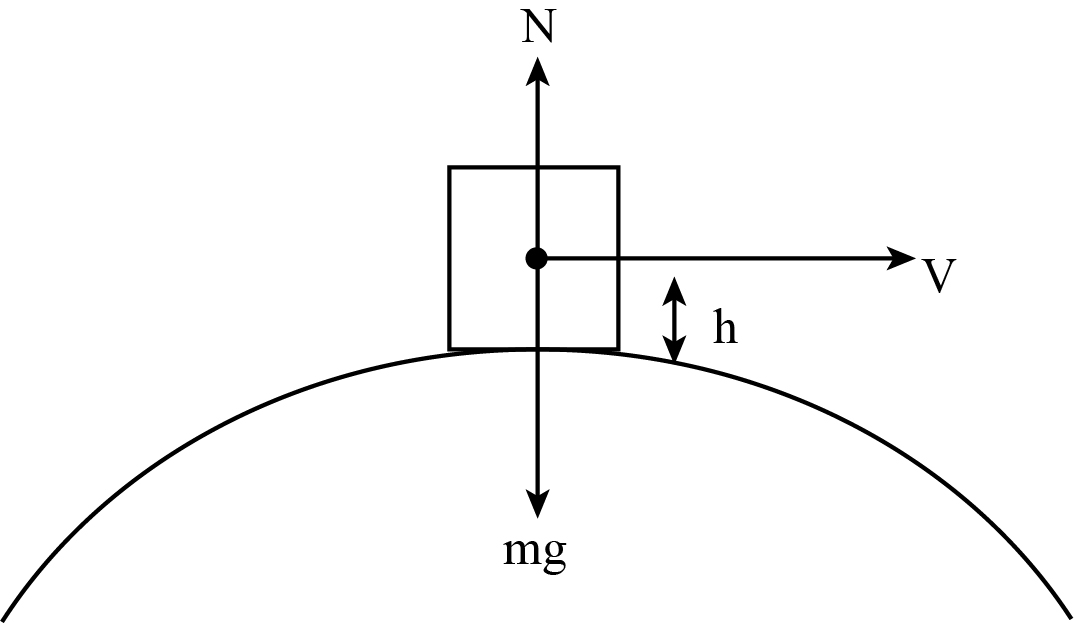
Express the condition for vertical equilibrium of a car while it is taking the turn.
$N + \dfrac{{m{V^2}}}{r} = mg$ …… (I)
Here $N$ is the normal reaction, $m$ is the mass of the vehicle, $r$ is the effective radius of turning and $g$ is the acceleration due to gravity. Here, $r = R + h$ .
Substitute $r = R + h$ in equation (I) to simplify the problem.
\[N + \dfrac{{m{V^2}}}{{R + h}} = mg\] ……. (II)
For the greatest speed of without losing the contact at road, the effective condition is N=0. Substitute $N = 0$ in equation (II) to find the value of $V$.
\[\begin{array}{l}
\dfrac{{m{V^2}}}{{R + h}} = mg\\
\dfrac{{{V^2}}}{{R + h}} = g\\
{V^2} = g\left( {R + h} \right)\\
V = \sqrt {g\left( {R + h} \right)}
\end{array}\]
Substitute 10 m/$s^2$ for $g$ , 8.9m for $R$ , 1.1 m for $r$ to find the value of $V$.
\[\begin{array}{l}
V = \sqrt {10\,{\rm{m/}}{{\rm{s}}^2}\left( {8.9{\rm{m}} + 1.1\,{\rm{m}}} \right)} \\
V = \sqrt {10\,{\rm{m/}}{{\rm{s}}^2} \times 10\,{\rm{m}}} \\
V = 10\,{\rm{m/s}}
\end{array}\]

Therefore, the correct option is (B).

Note: The greatest speed is achieved when the car will leave the ground. As the normal reaction is offered by the surface to the body and when the body leaves the ground then no force is offered by the ground to the body and hence $N = 0$.