Question

The vectors, vector AB = 3i + 4k and vector AC = 5i - 2j + 4k are the sides of a triangle ABC. The length of the median through A is
(a) \[\sqrt {72} \]
(b) \[\sqrt {33} \]
(c) \[\sqrt {288} \]
(d) \[\sqrt {18} \]

Answer 1

Hint: Here, we will draw the figure and take point D as the mid-point between point B and point C of the given triangle ABC where we take A as the origin. Since, a median of the triangle divides the opposite side into two equal parts. Thus, using this formula we will find the median i.e. AD value. Lastly, by substituting the values in the formula of the length of the median to get the final output.

Complete step by step solution:
Given that, we have a triangle ABC.
Let us take point A as the origin i.e. A (0, 0)
The vectors given are as below:
First, the \[\overrightarrow {AB} \] is equal to the position vector of \[\overrightarrow B \].
\[\therefore \overrightarrow {AB} = 3i + 4k\]
So, the coordinate of B is (3, 0, 4).
Next, the \[\overrightarrow {AC} \] is equal to the position vector of \[\overrightarrow C \].
\[\therefore \overrightarrow {AC} = 5i - 2j + 4k\]
So, the coordinate of C is (5, -2, 4).
Since, a line segment that joins any vertex of the triangle and the mid-point of its opposite side is called a median.
According to the given information, the figure is drawn as below:

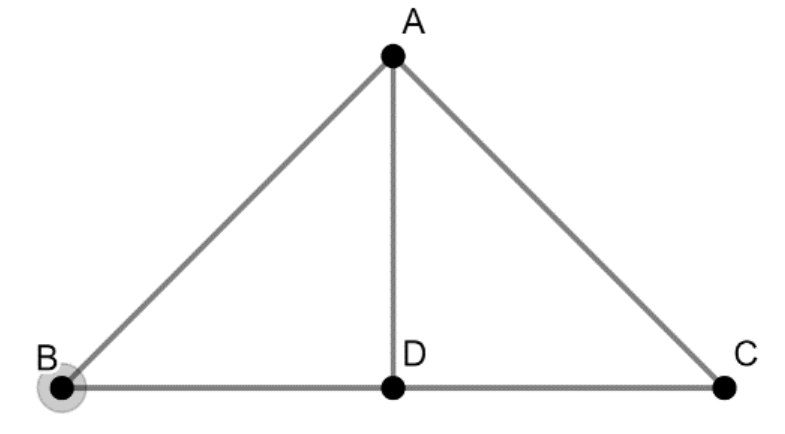
Thus, the position vector of midpoint of \[\overrightarrow B \] and \[\overrightarrow C \] is \[\overrightarrow D \].
\[\therefore \overrightarrow D = \dfrac{{\overrightarrow {AB} + \overrightarrow {AC} }}{2}\]
Substituting the given values, we will get,
\[ \Rightarrow \overrightarrow D = (\dfrac{{3 + 5}}{2})\widehat i + (\dfrac{{0 - 2}}{2})\widehat j + (\dfrac{{4 + 4}}{2})\widehat k\]
On evaluating this, we will get,
\[ \Rightarrow \overrightarrow D = 4\widehat i - \widehat j + 4\widehat k\]
So, the midpoint of BC can be easily found by the midpoint formula of two points as D (4, -1, 4).
Thus, the value of the median is:
\[\overrightarrow {AD} = 4\widehat i - \widehat j + 4\widehat k\]
Now, the length of the median through A is \[\sqrt {33} \].
\[\left| {AD} \right|\]
\[ = \sqrt {{{(4 - 0)}^2} + {{( - 1 - 0)}^2} + {{(4 - 0)}^2}} \]
Removing the bracket, we will get,
\[ = \sqrt {{4^2} + {{( - 1)}^2} + {4^2}} \]
On evaluating this above expression, we will get,
\[ = \sqrt {16 + 1 + 16} \]
\[ = \sqrt {33} \]

Hence, the length of the median is $\sqrt {33}$. So, option (B) is correct.

Note:
This question would become easy to solve if you notice the similarity between parallelogram law of vector addition and the fact that the diagonal represents the resultant vector and also the diagonals bisects each other. Let us assume the resultant of vector AC and AB is vector AD. As we know diagonals bisect each other. Hence half of the resultant vector AD will be the median for side BC.