Question

The vector 3-4i is turned anticlockwise through an angle of ${{180}^{\circ }}$ and stretched 2.5 times. The complex number corresponding to the newly obtained vector is ..
\[\begin{align}
  & A.\dfrac{-15}{2}+10i \\
 & B.\dfrac{15}{2}+10i \\
 & C.\dfrac{-15}{2}-10i \\
 & D.\dfrac{15}{2}-10i \\
\end{align}\]

Answer 1

Hint: For solving this question, we first need to understand the signs in the complex plane. Since every complex plane is of the form x+iy. So a complex plane is the same as an argand plane where x is x and y is y axis. First we will find the quadrant in which the current vector is lying. Then we will find the quadrant if the vector is rotated through an angle ${{180}^{\circ }}$. Using the quadrant, we will change the sign of the vector and at last we will multiply obtained vector by 2.5 to get the required vector.

Complete step-by-step answer:
Let us understand the complex plane first. In the complex plane the horizontal axis is the x axis and vertical axis is y axis. It looks like this:

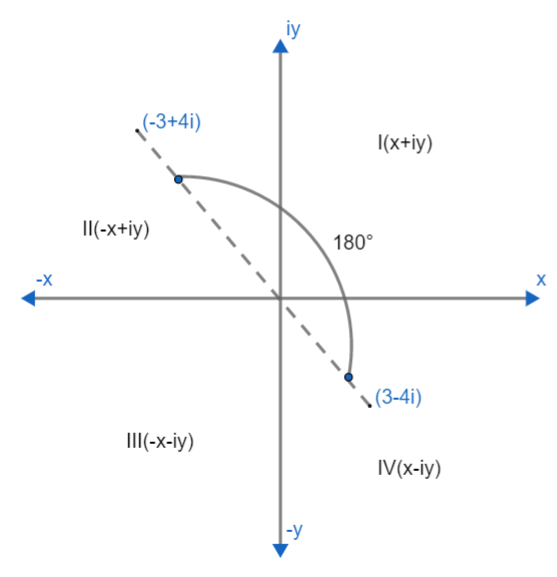
Complex numbers of the form x+iy lie in I quadrant, -x+iy lie in II quadrant, -x-iy lies in III quadrant and x-iy lies in IV quadrant.
Here we are given complex numbers as 3-4i. It is of the form x-iy. So it lies in the IV quadrant. If we turn the vector anticlockwise to ${{180}^{\circ }}$ our new vector will lie in II quadrant where vectors are of form -x+iy. So our vector becomes -3+4i.
Now, we have to stretch it 2.5 times, so our new vector becomes 2.5 times the original vector. So required complex number will be,
\[\begin{align}
  & \Rightarrow 2.5\left( -3+4i \right) \\
 & \Rightarrow \left( -2.5\times 3 \right)+\left( 2.5\times 4 \right)i \\
 & \Rightarrow \left( \dfrac{-25\times 3}{10} \right)+\left( \dfrac{25\times 4}{10} \right)i \\
 & \Rightarrow \dfrac{-15}{2}+10i \\
\end{align}\]
Hence, $\dfrac{-15}{2}+10i$ is our required vector.

So, the correct answer is “Option A”.

Note: Here students can make mistakes in positive and negative signs in quadrant. While changing quadrants, make sure that numbers remain the same and only sign changes. While selecting a vector, make sure 2.5 is multiplied with both -3 and 4. Complex plane is just like argand plane.