Question

The value on net force on charge ${Q_0}$

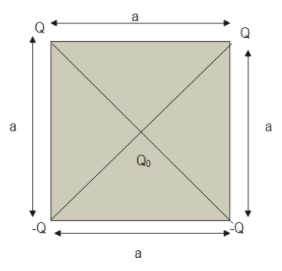
Answer 1

Hint: In this question we will use the relation of electrostatic force between the charges and the distance between them. Also, by applying the formula and calculating step by step, we get the required result. At last we will discuss the basics of electrostatic force and also mechanical force.
Formula used:
$F = \dfrac{{kQ{Q_0}}}{{{a^2}}}$

Complete answer:

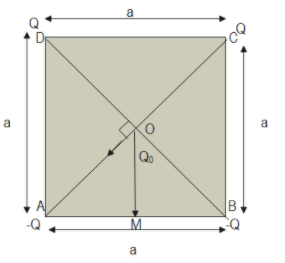
Here we can know that the force due to charge Q at D and B along DB is given as:
$F' = {F_D} + {F_B}$
As we know, force is given by:
$F' = \dfrac{{kQ{Q_0}}}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \dfrac{{k( + Q){Q_0}}}{{{{\left( {a\sqrt 2 } \right)}^2}}}$
Here, Q and ${Q_0}$ are charges, a is distance between the two charges, k is known as Coulomb’s law constant having value $9 \times {10^9}N{m^2}/{C^2}$
Further, solving we get:
$\eqalign{& \Rightarrow F' = 2 \times 2\dfrac{{kQ{Q_0}}}{{{a^2}}} \cr
  & \Rightarrow F' = 4\dfrac{{kQ{Q_0}}}{{{a^2}}} \cr} $
Similarly the force along CA, due to charge Q and ${Q_0}$ at A and C will be given as:
$F'' = {F_A} + {F_C}$
$ \Rightarrow F'' = 4\dfrac{{kQ{Q_0}}}{{{a^2}}}$
Now, resultant force will be along OM, which is given as:
${F_R} = \sqrt {{{(F')}^2} + {{(F'')}^2} + 2(F'F'')cos{{90}^ \circ }} $
By substituting the value of forces in above equation, we get:
$\eqalign{& \Rightarrow {F_R} = \sqrt {{{\left( {4\dfrac{{kQ{Q_0}}}{{{a^2}}}} \right)}^2} + {{\left( {4\dfrac{{kQ{Q_0}}}{{{a^2}}}} \right)}^2} + 0} \cr
  & \Rightarrow {F_R} = \sqrt 2 \times 4\dfrac{{kQ{Q_0}}}{{{a^2}}} \cr
  & \therefore {F_R} = 4\sqrt 2 \dfrac{{kQ{Q_0}}}{{{a^2}}} \cr} $
Therefore, we get the required result in above equation, which gives expression of net force on charge ${Q_0}$

Additional information:
Electrostatic force is also known as Coulomb force. It is defined as the attractive or repulsive forces between two electrical charges attract each other. Also, mathematically it is proportional to the ratio of product of the two charges and distance between the two charges.
Further we also know that force is simply any push or pull. The S.I unit of force is Newton represented by N. The acceleration is defined as the increase in the velocity of an object. The acceleration is measured in meters per Second Square.
There are three laws of motions given by Newton. These laws of motion relate an object's motion to the forces acting on it.
First law of motion states that an object continues to be in rest or in motion in a particular direction until and unless any external force is applied on it.
 In the second law of motion, the force on an object is equal to its mass times its acceleration. This law also gives the relation of momentum and force.
In the third law of motion, every action has an equal and opposite reaction.

Note:
Here, we should remember that the magnitude of charges is only taken in calculation. The S.I unit of charge is Coulomb. Further, Force applied on an object changes its motion, speed, direction and also its shape. There is a very small difference between the force applied and the pressure applied on an object. Pressure is always given as the force per unit area.