Question

The value of effective resistance between $A$ and $B$ is? $\left( {Given\,\,R = 2k\Omega } \right)$

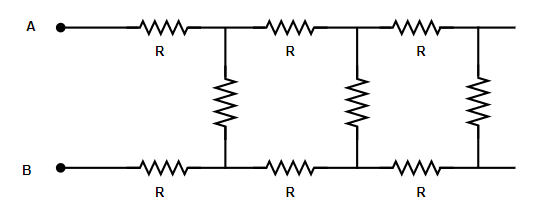
\[\left( a \right)\,\,(1 + \sqrt 3 )k\Omega \]
\[\left( b \right)\,\,2(1 + \sqrt 3 )k\Omega \]
\[\left( c \right)\,\,(1 - \sqrt 3 )k\Omega \]
\[\left( d \right)\,\,2(1 - \sqrt 3 )k\Omega \]

Answer 1

Hint: Whenever you are given with a question where resistances or capacitances are connected in a similar pattern up to $'n'$ number of times, firstly find unit cell of the network then assume x or y as the combined resistance for the rest of pattern $\left( {n - 1} \right)$ number of times. This pattern is also known as the infinite ladder network.
Formula used:
(A) \[r = {r_1} + {r_2} + {r_3} + ........... + {r_n}\] (when resistance are connected in series)
(B) \[\dfrac{1}{r} = \dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}} + \dfrac{1}{{{r_3}}} + ............. + \dfrac{1}{{{r_n}}}\] (when resistance are connected in parallel)

Complete step by step answer:
Let us assume that equivalent resistance or effective resistance for this network is \[{R_{eq}}\] . Here, in this problem, the unit cell of network is shown in below picture as follows:

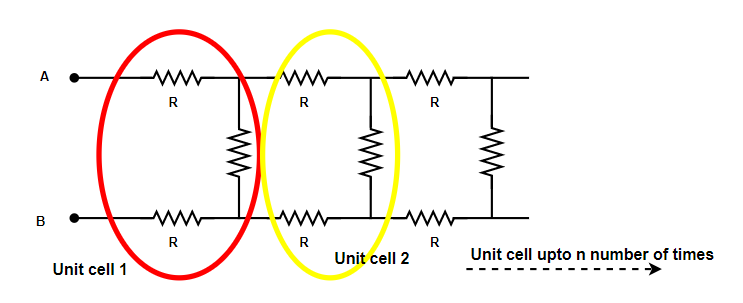
Thus, your first basic step in the question is to find a unit cell of the network in circuit.
Let the combined resistance for the rest of the network (except the resistance of unit cell 1) be $x$ .
\[ \Rightarrow {R_{AB}} = x\]
Where, \[{R_{AB}}\] is equal to the combined resistance of $\left( {n - 1} \right)$ unit cells.

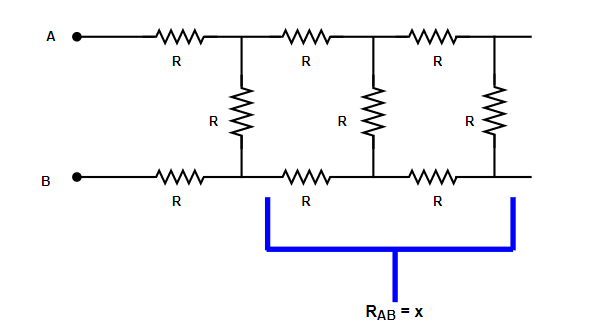
Then,

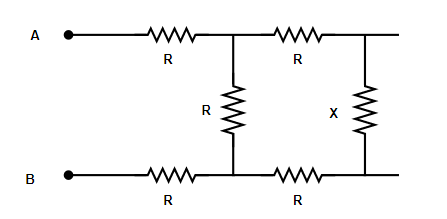
Also,

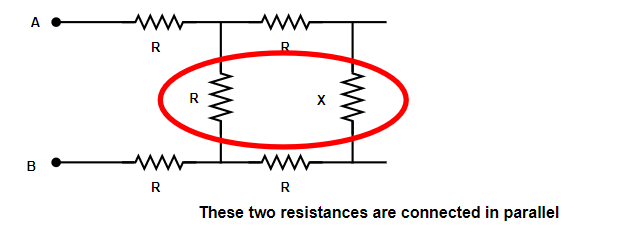
From the figure, the combined resistance $r$ for parallel combination is given by
\[\dfrac{1}{r} = \dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}} + \dfrac{1}{{{r_3}}} + ............. + \dfrac{1}{{{r_n}}}\] (When resistance are connected in parallel)
And it can be written as
\[ \Rightarrow \dfrac{1}{r} = \dfrac{1}{R} + \dfrac{1}{x}\]
Now on solving it, we get
\[ \Rightarrow \dfrac{1}{r} = \dfrac{{x + R}}{{xR}}\]
Solving it, we get
\[ \Rightarrow r = \dfrac{{xR}}{{x + R}}\] and we will let it eq. $1$

Next, from the below shown figure, it’s clear that all the three resistances are in connected in series,

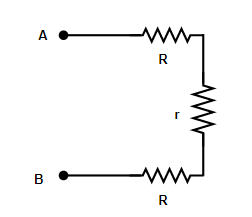
\[\therefore \] By applying, \[r = {r_1} + {r_2} + {r_3} + ........... + {r_n}\] (when resistance are connected in series) we get,${R_{eq}} = R + r + R$ and we will let it eq. $2$
Also, given in question that, $R = 2K\Omega $ and from above eq. $1$ , substituting values in eq. $2$ , we get as follows:
\[ \Rightarrow {R_{eq}} = 2 + \dfrac{{2x}}{{2 + x}} + 2\]
And on solving it, we get
\[ \Rightarrow {R_{eq}} = 4 + \dfrac{{2x}}{{2 + x}}\]
Now, \[{R_{eq}} \approx {R_{AB}}\]
\[ \Rightarrow {R_{eq}} = x\] , thus
\[ \Rightarrow x = 4 + \dfrac{{2x}}{{2 + x}}\]
Now on doing the cross multiplication, we get
\[ \Rightarrow x\left( {2 + x} \right) = 4\left( {2 + x} \right) + 2x\]
And on solving it, we get
\[ \Rightarrow 2x + {x^2} = 8 + 4x + 2x\]
Further doing the solution,
\[ \Rightarrow {x^2} = 8 + 4x\]
Or it can be written as
\[ \Rightarrow {x^2} - 4x - 8 = 0\]
By applying the formula for finding roots of a quadratic equation, \[\dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\] , We get,
\[ \Rightarrow \dfrac{{4 \pm \sqrt {16 + 32} }}{2}\]
On solving it,
\[ \Rightarrow \dfrac{{4 \pm \sqrt {48} }}{2}\]
And it will be equal to
\[ \Rightarrow 2(1 \pm \sqrt 3 )\]
Now the value of \[\sqrt 3 = 1.7320\], so \[1 - \sqrt 3 \] have negative value, and resistance can’t have a negative value.
\[\therefore x = 2(1 + \sqrt 3 )\] would be the effective resistance to give an infinite ladder network.

\[ \Rightarrow \] Option $\left( b \right)$ is correct.

Note: Do not confuse yourself with why we put\[{R_{eq}} \approx {R_{AB}}\] , because ladder continues up to infinity, therefore, resistance of $1unit$ cell would be very-very small and can be negligible. Always, consider the positive value of resistance instead a negative value. Try to simplify the network step by step to reduce any error.