Question

The value of ‘c’ in Lagrange’s mean value theorem for ${\text{f(x) = logx}}$ on ${\text{[1,e]}}$ is
A) $\dfrac{{\text{e}}}{{\text{2}}}$
B) ${\text{e - 1}}$
C) ${\text{e - 2}}$
D) ${\text{1 - e}}$

Answer 1

Hint: We can find the value of ${\text{f'}}\left( {\text{c}} \right)$using Lagrange’s mean value theorem. We can find the value of ${\text{f'}}\left( {\text{c}} \right)$by taking the derivative of the function and substituting c to it. Then we can compare the two values and solve for c.

Complete step by step solution: According to Lagrange’s mean value theorem, if a function ${\text{f}}\left( {\text{x}} \right)$ is continuous in the interval $\left[ {{\text{a,b}}} \right]$, and differentiable in $\left( {{\text{a,b}}} \right)$, then there will be at least one point c in the interval $\left[ {{\text{a,b}}} \right]$such that
${\text{f'}}\left( {\text{c}} \right){\text{ = }}\dfrac{{{\text{f}}\left( {\text{b}} \right){\text{ - f}}\left( {\text{a}} \right)}}{{{\text{b - a}}}}$
We have the function ${\text{f(x) = logx}}$.
Firstly, we can check the continuity of the function. For that, we can draw the graph of the function

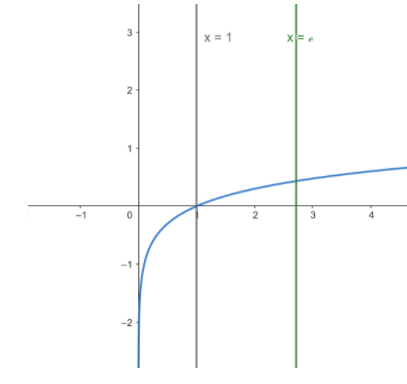
From the graph, we can see that the function is well defined and continuous in the given interval of ${\text{[1,e]}}$.
Taking the derivative of the function, we get,
${\text{f'}}\left( {\text{x}} \right){\text{ = }}\dfrac{{\text{1}}}{{\text{x}}}$
${\text{f'}}\left( {\text{x}} \right)$exists for all values of x in the given interval. So the function is differentiable in the given interval.
On substituting ${\text{x = c}}$in the derivative, we get,
$ \Rightarrow {\text{f'}}\left( {\text{c}} \right){\text{ = }}\dfrac{{\text{1}}}{{\text{c}}}$ … (1)
By Lagrange’s mean value theorem on the interval ${\text{[1,e]}}$,
${\text{f'}}\left( {\text{c}} \right){\text{ = }}\dfrac{{{\text{f}}\left( {\text{b}} \right){\text{ - f}}\left( {\text{a}} \right)}}{{{\text{b - a}}}}{\text{ = }}\dfrac{{{\text{f}}\left( {\text{e}} \right){\text{ - f}}\left( {\text{1}} \right)}}{{{\text{e - 1}}}}{\text{ = }}\dfrac{{{\text{loge - log1}}}}{{{\text{e - 1}}}}$
We know that, ${\text{lo}}{{\text{g}}_{\text{e}}}\left( {{{\text{e}}^{\text{1}}}} \right){\text{ = 1}}$ and ${\text{lo}}{{\text{g}}_{\text{e}}}\left( {\text{1}} \right){\text{ = lo}}{{\text{g}}_{\text{e}}}\left( {{{\text{e}}^{\text{0}}}} \right){\text{ = 0}}$. So we get,
${\text{f'}}\left( {\text{c}} \right){\text{ = }}\dfrac{{{\text{1 - 0}}}}{{{\text{e - 1}}}}$
${\text{f'}}\left( {\text{c}} \right){\text{ = }}\dfrac{{\text{1}}}{{{\text{e - 1}}}}$ … (2)
Equating equations (1) and (2), we get,
$\dfrac{{\text{1}}}{{\text{c}}}{\text{ = }}\dfrac{{\text{1}}}{{{\text{e - 1}}}}$
Solving for c, we get,
${\text{c = e - 1}}$
The required value of c is e-1.

Therefore, the correct answer is option B.

Note: Lagrange’s mean value theorem is applicable only for functions that are continuous in the given interval. The function must be also differentiable in the same open interval. We must make sure that the given function is continuous and differentiable in the given interval. We must know the derivatives of basic functions to solve this type of problems. Lagrange’s mean value theorem can be verified by drawing the graph of the function in the given interval.