Question

The two triangles in the figure are congruent by the congruence theorem. Here, it is given $OQ = OR$. Which of the following conditions, along with the given condition, is sufficient to prove that the two triangles are congruent to each other?

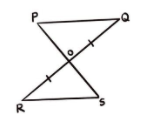
A.$\angle P = \angle S$
B.$\angle Q = \angle R$
C.$OP = OS$
D.$PQ = SR$

Answer 1

Hint: Congruence can be proved by SSS(side-side-side), SAS(side-angle-side), ASA(angle-side-angle) and AAS(angle-angle-side), where S denotes Side and A denotes Angle. Check which one of these is applicable for this question and then use it to prove that both triangles are congruent to each other.

Complete step-by-step answer:
It is given in the question that one pair of sides are equal.
If we use the SSS convention, the two other sufficient conditions would be option C and D. That is, all three pairs of sides of both the triangles are equal. And if all three sides are equal, the two triangles are bound to be congruent.
We cannot use SAS and ASA because with the available options, we cannot make any combination where two pairs of sides and their included angle are equal or two pairs of angles and their included side are equal.
We cannot use AAS either because the non included sides $OR$ and $OQ$ are not the same non included side corresponding to $\angle R,\angle S$ and $\angle P,\angle Q$. By not the same non-included side, we mean that the relative positions of these two sides are not the same corresponding to their angle pairs.
Hence the correct option is C and D.

Note: Do not get confused by the meanings of the notations SSS, SAS, ASA and AAS. SSS means having all three pairs of sides equal. SAS means having two pairs of sides and their included angle equal. ASA means having two pairs of angles and their included side equal and AAS means having two pairs of angles and the non-included side equal. To solve such questions, check each one of these conditions separately to see which one is being satisfied.