Question

The two ends A and B of a uniform rod of length l=1m are moving with velocities ​ ${{V}_{A}}$ and ${{V}_{B}}$​ as shown.

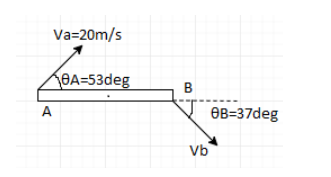
The velocity ${{V}_{B}}$ ​ is:
A: 25m/s
B: 15m/s
C:20m/s
D: 50m/s

Answer 1

Hint: According to the problem, the length of the rod is given, velocities are also given. We have to resolve the velocities along the required directions and deduce the necessary value from the resultant forces and the components. Since one value of velocity and the angles are given, we can easily find the other values as well.

Complete step by step solution:
We take a purely geometric method to approach this question. We don’t need to look into any pre-existing formulae. Instead, we can resolve the given vector quantities into components.
The reconstructed diagram is as follows:

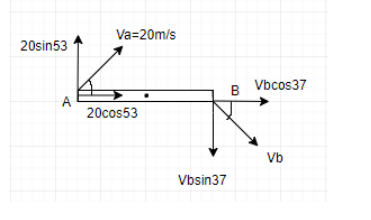
We have resolved ${{V}_{A}}$ and ${{V}_{B}}$to its horizontal and vertical components along the x and y axis.
We’re given that velocity at A is 20m/s and velocity at B is ${{V}_{B}}$
Horizontal component of ${{V}_{A}}$ is given by ${{V}_{A}}\cos 53=20\times \dfrac{3}{5}=12m/s$
Horizontal component of ${{V}_{B}}$ is given by
$
 {{V}_{B}}\cos 37 = {{V}_{B}}\times \dfrac{4}{5} \\
$
Equating both components,
$
 12=\dfrac{4{{V}_{B}}}{5} \\
 \Rightarrow {{V}_{B}}=\dfrac{60}{4}=15m/s \\
$
Hence the value of velocity acting at the point B is 15m/s.

Therefore, option (B) is the correct answer.

Note: For any vector, there are two rectangular components: the horizontal component and the vertical component and these two vectors add up to give the resultant value of the vector. The horizontal component is along the x axis and the vertical component is along the y axis. In other words we can say that if the light is shining from above, then the shadow that forms down is the horizontal component and if the light is from the side, the shadow formed on the opposite side is the vertical component.