Question

The transformation ratio in the step-up transformer is
A. 1
B. Greater than one
C. Less than one
D. The ratio greater or less than one depends on the other factors

Answer 1

Hint: The working of the transformer is based on the principle of mutual induction. It is defined as “the emf generated in the coil caused due to change of flux in the other coil”.

Formula Used:
Transformation Ratio = $\dfrac{{{U_2}}}{{{U_1}}} = \dfrac{{{N_2}}}{{{N_1}}}$

Complete step by step answer:

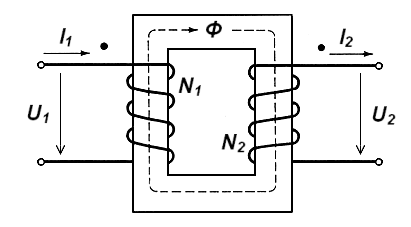
The transformer consists of two coils wound on a soft-core. They are completely insulated from each other. The coil on the left is called the primary coil where the input AC voltage is applied. The coil on the right is called secondary coil where the output AC voltage is realised.
The number of turns on these coils are not the same. These coils are wound differently, based on the purpose of the transformation. The number of turns in the primary coil is ${N_1}$and the number of turns in the secondary coil is ${N_2}$.
When the input voltage ${U_1}$is applied on the input coil, there is emf generated on the second coil due to mutual inductance.
${U_2} = - {N_2}\dfrac{{d\phi }}{{dt}}$
where $\dfrac{{d\phi }}{{dt}}$ is the rate of change of magnetic flux.
There is an emf induced in the primary coil due to change in the magnetic flux linked to the same coil. This is called a back emf.
${U_1} = - {N_1}\dfrac{{d\phi }}{{dt}}$

Thus,
$\dfrac{{{U_2}}}{{{U_1}}} = \dfrac{{{N_2}}}{{{N_1}}}$
This implies that the induced voltage in the secondary coil depends on the ratio of turns in the 2 coils. This ratio is called the transformation ratio.
The purpose of a step-up transformer to increase the voltage. Thus, in a step-up transformer, the output voltage is higher than the input voltage. In such cases, the transformation ratio –
$\dfrac{{{U_2}}}{{{U_1}}} = \dfrac{{{N_2}}}{{{N_1}}} > 1$
Hence, the correct option is Option B.

Note:
You might have a common confusion in transformers, as to how the voltage is increased from a very small number to a huge number in the case of a step-up transformer. The answer for this doubt is –
The voltage increases from a small number to a huge number at the expense of a huge decrease in current.
This is because, in the transformer, the output power must be equal to input power (assuming the ideal scenario without any power loss)
We know that,
$
  P = VI \\
  {P_1} = {P_2} \\
 $
Therefore, $VI$= constant
$ \to V \propto \dfrac{1}{I}$
Thus, if voltage increases from a small number to a huge number, the current decreases drastically, from a higher number to a lower number so as to balance the product of voltage and current on either side of the coil.