Question

The total deviation of the incident ray when it emerges out of the prism is:

 $ \left( A \right){30^ \circ } \\
  \left( B \right){60^ \circ } \\
  \left( C \right){90^ \circ } \\
  \left( D \right){45^ \circ } \\ $

Answer 1

Hint :In order to solve this question, we are going to first see the formula for the angle of deviation for the prism, then constructing figure for the overall scenario of the rays entering and the emerging rays, the equations are simplified for the angle of the prism and the angle of deviation, the question is solved.

Complete Step By Step Answer:
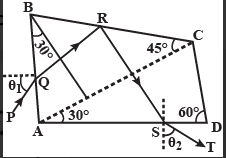
As we can see in this question, we are given with the figure, wherein the ray $ P $ hits the points at $ Q,R,S $ and emerges from the point as the ray $ T $
Let us construct another figure that shows the overall scenario
 

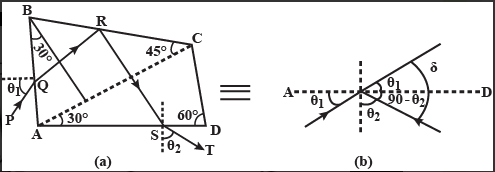
The deviation is given by
 $ \delta = 90 - {\theta _2} + {\theta _1} $
In the prism, $ DAC $ as it is given that the angle of the prism is
 $ A = {30^ \circ } $
Using the angle of prism formula, i.e.
 $ A = {r_2} + r' $
Therefore, putting the values, we get
 $ {30^ \circ } = {r_2} + {0^ \circ } \\
   \Rightarrow {r_2} = {30^ \circ } \\ $
Given: the refractive index of the prism is given by
 $ n = 2\sin {\theta _1} $
If we use the Snell’s law at the point S, then,
 $ 1 \times \sin {\theta _2} = n \times \sin {r_2} $
Calculating the value of $ \sin {\theta _2} $ , then,
 $ \sin {\theta _2} = 2\sin {\theta _1} \times \sin {30^ \circ } $
Thus, we get
 $ \sin {\theta _2} = \sin {\theta _1} $
Now, if the sines of the angles is same, then, this implies that, the angles are also equal
 $ {\theta _1} = {\theta _2} $
Now putting this relation in the equation for the angle of deviation,
 $ \begin{gathered}
  \delta = 90 - {\theta _2} + {\theta _1} \\
   \Rightarrow \delta = {90^ \circ } \\
\end{gathered} $
Hence, option $ \left( C \right){90^ \circ } $ is the correct answer.

Note :
The two prisms that are joined from the bases side to form a parallelogram, then, the incident rays are reflected multiple times and the final ray emerges from the one side of the second prism.
The total deviation thus produced depends on the angles, i.e. angle of incidence and deviation.