Question

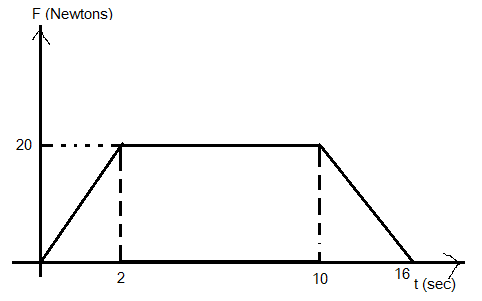
The thrust (F) versus time graph of a rocket is shown in the figure. The mass of the rocket is 1200g. Then the velocity of the rocket after 16 seconds starting from rest (Neglect the gravity)

A. \[300\dfrac{m}{s}\]
B. \[200\sqrt 2 \dfrac{m}{s}\]
C. \[100\dfrac{m}{s}\]
D. \[200\dfrac{m}{s}\]

Answer 1

Hint: In the given question, change the force-time curve into the acceleration-time curve since acceleration is the change in velocity of time by using newton’s second law of motion. Newton’s second law of motion states the acceleration of an object produced by a net force is proportional to the mass of that object. For the result, we need to find the area under the acceleration-time curve.

Complete step by step answer:
Given the mass of the rocket is 1200 grams and from the figure, it can be observed that the maximum force is 20 newton. From the newton’s second law of motion, we can write, \[F = ma\]
Substitute 1200 grams (or 1200/1000 kilograms) for mass and 20 newtons for the force in the formula \[F = ma\] to determine the acceleration of the rocket.
\[
  F = ma \\
  a = \dfrac{F}{m} \\
   = \dfrac{{20}}{{\left( {\dfrac{{1200}}{{1000}}} \right)}} \\
   = \dfrac{{20}}{{1.2}} \\
   = \dfrac{{50}}{3} \\
 \]
Now we can draw acceleration time graph as

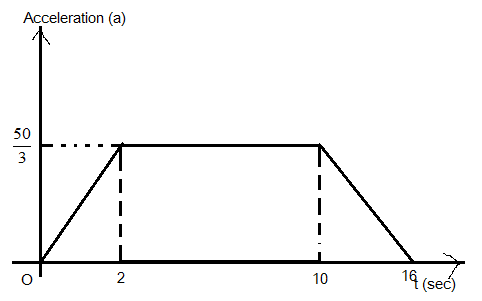
Now the area in the acceleration-time graph changes with velocity hence we can say
Change in velocity= area under the graph which equals to the area of the rectangle and two areas of the triangles.
$`
  v - u = \left( {\dfrac{1}{2} \times \dfrac{{50}}{3} \times 2} \right) + \left( {\dfrac{{50}}{3} \times \left( {10 - 2} \right)} \right) + \left( {\dfrac{1}{2} \times \dfrac{{50}}{3} \times \left( {16 - 10} \right)} \right) \\
  v - u = \left( {\dfrac{1}{2} \times \dfrac{{50}}{3} \times 2} \right) + \left( {\dfrac{{50}}{3} \times 8} \right) + \left( {\dfrac{1}{2} \times \dfrac{{50}}{3} \times 6} \right) \\
\implies v - u = \dfrac{{50}}{3}\left[ {1 + 8 + 3} \right] \\
\implies v - u = \dfrac{{50}}{3} \times 12 \\
 \implies v - u = 50 \times 4 \\
\implies v - u = 200{\text{ m/sec}} \\
$
Since the objects start from rest so we can say \[u = 0\]
Hence the velocity of the rocket will be
\[
  v - 0 = 200{\text{ m/sec}} \\
  v = 200{\text{ m/sec}} \\
 \]
Therefore the velocity of the rocket after 16 seconds starting from rest is \[200{\text{ m/sec}}\].
So, the correct answer is “Option D”.

Note:
As we know the area under a curve is the same as the definite integral between two fixed points hence we can also use the method of integration to find the change in momentum. Moreover, the given curve is between thrust (force) and the time but we need the velocity which can be determined by the acceleration-time curve, so it should be transformed accordingly.