Question

The terminals of a 18V battery with an internal resistance of 1.5Ω are connected to a circular wire of resistance 24Ω at two points distant at one quarter of the circumference of a circular wire. The current through the bigger arc of the circle will be
A) 0.75A
B) 1.5A
C) 2.25A
D) 3A

Answer 1

Hint
Refer the diagram the circuit is initially in parallel. We can find out the resistances of the smaller arc and larger arc and then the equivalent current in the circuit. After doing so we can apply the current resistance inverse relationship to solve the problem.

Complete step by step answer

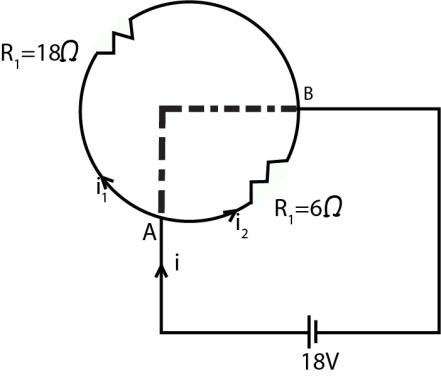
Given that the terminal is connected at one quarter distance.
It means that the circuit is now a parallel one consisting of two branches having the same common potential and it is given that the value of that potential is 18V.
As said that the total resistance is $24\Omega $ of the entire circle so of one quarter circle it should be $\dfrac{{24}}{4} = 6\Omega $ as a quarter means $\dfrac{1}{4}$th of a circle.
And the resistance of the other part must be $24 - 6 = 18\Omega $.
Since the potential across ${R_1}\,{\text{and}}\,{R_2}$ is the same, so they both are parallel.
Hence their equivalent resistance becomes $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Putting the values we get,
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{18}} + \dfrac{1}{6} $
$\Rightarrow {R_{eq}} = \dfrac{{6 \times 18}}{{6 + 18}} $
$\Rightarrow {R_{eq}} = 4.5\Omega $
Now it is also given that the internal Resistance of the cell is $1.5\Omega $.
Hence the net equivalent resistance is $1.5 + 4.5 = 6\Omega $
So, the net current in the circuit will be $I = \dfrac{V}{R} = \dfrac{{18}}{6} = 3A$.
We know that the current in parallel resistance is distributed in an inverse ratio of resistance.
Current through bigger arc is given by,
${I_1} = \dfrac{{{R_1}}}{{{R_1} + {R_2}}}I$
On putting the values and further solving we get,
$\Rightarrow {I_1} = \dfrac{6}{{24}} \times 3 $
$\Rightarrow {I_1} = 0.75A $
Hence the current in the bigger arc is given by ${I_1} = 0.75A$and so the correct option is option (A).

Note
We can further apply the same formula of inverse current resistance relationship to find out the value of ${I_2}$(current in the smaller arc, however it is advised to use KCL always to do so as it becomes easier to solve. Like in this example the current in smaller loop can be found out by KCL and we have,
${I_2} = I - {I_1} $
$\Rightarrow {I_2} = 3 - 0.75 = 2.25A $