Question

The tangents at two points, P and Q, of a conic meet at T and S is the focus. Prove that if the conic be a parabola, then \[{\rm{S}}{{\rm{T}}^2} = {\rm{SP}} \cdot {\rm{SQ}}\].

Answer 1

Hint:
Here we have to use the properties of the trigonometry and polar form of the parabola. Firstly, we will write the equation of the parabola in the polar form and simplify it. Then we will write the equation of the tangent at P and Q meets at T in the polar form at its polar coordinates. We will then simplify the equation to prove the given equation.

Complete step by step solution:
It is given that tangents at two points, P and Q, of a conic meet at T and S is the focus.

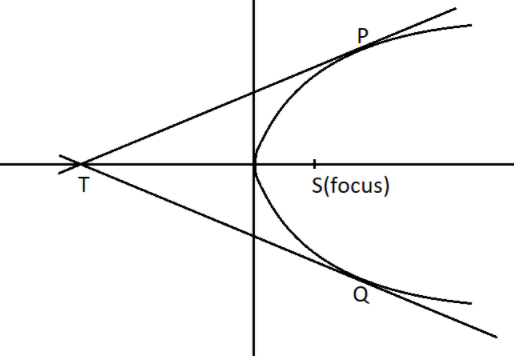
Firstly, we will write the equation of the parabola in the polar form.
\[\dfrac{{2a}}{r} = 1 - \cos \theta \]
By using the property \[1 - \cos \theta = 2{\sin ^2}\dfrac{\theta }{2}\] we can write the equation as
\[\begin{array}{l}\dfrac{{2a}}{r} = 2{\sin ^2}\dfrac{\theta }{2}\\ \Rightarrow \dfrac{{2a}}{{2{{\sin }^2}\dfrac{\theta }{2}}} = r\end{array}\]
On simplification, we get
\[ \Rightarrow r = a\cos e{c^2}\dfrac{\theta }{2}\]
Now, let us assume that the vectorial angle of P and Q be \[\alpha \] and \[\beta \] respectively. Therefore we get
\[ \Rightarrow {\rm{SP}} = a\cos e{c^2}\dfrac{\alpha }{2}\]
\[ \Rightarrow {\rm{SQ}} = a\cos e{c^2}\dfrac{\beta }{2}\]
Now we have to write the equation of the tangent at P and Q that meets at T in the polar form at its polar coordinates.
Let us assume that the polar coordinates of the tangent be \[(r',\phi )\]. Therefore, we get
\[ \Rightarrow \dfrac{{2a}}{{r'}} = \cos (\phi - \alpha ) - \cos \phi \]……….. (1)
\[ \Rightarrow \dfrac{{2a}}{{r'}} = \cos (\phi - \beta ) - \cos \phi \]……….. (2)
Now by solving the equation (1) and (2) we get
\[ \Rightarrow \cos (\phi - \alpha ) = \cos (\phi - \beta )\]
\[ \Rightarrow \phi - \alpha = \phi - \beta \]
\[ \Rightarrow \phi = \dfrac{{\alpha + \beta }}{2}\]
Now we will substitute the value of\[\phi \] in the equation (1). So, we get
\[ \Rightarrow \dfrac{{2a}}{{r'}} = \cos (\dfrac{{\alpha + \beta }}{2} - \alpha ) - \cos \dfrac{{\alpha + \beta }}{2}\]
\[ \Rightarrow \dfrac{{2a}}{{r'}} = \cos (\dfrac{{\alpha - \beta }}{2}) - \cos \dfrac{{\alpha + \beta }}{2}\]
Now by using the property of trigonometry, \[\cos \dfrac{{a - b}}{2} - \cos \dfrac{{a + b}}{2} = 2\sin \dfrac{a}{2}\sin \dfrac{b}{2}\], we can rewrite above equation as
\[ \Rightarrow \dfrac{{2a}}{{r'}} = 2\sin \dfrac{\alpha }{2}\sin \dfrac{\beta }{2}\]
We can write \[r'\]as ST.
\[ \Rightarrow \dfrac{a}{{ST}} = \sin \dfrac{\alpha }{2}\sin \dfrac{\beta }{2}\]
\[ \Rightarrow {\rm{ST}} = a{\rm{ }}\cos ec\dfrac{\alpha }{2}\cos ec\dfrac{\beta }{2}\]
Now squaring both sides, we get
\[ \Rightarrow {\rm{S}}{{\rm{T}}^2} = {a^2}{\rm{ }}\cos e{c^2}\dfrac{\alpha }{2}\cos e{c^2}\dfrac{\beta }{2}\]
We can write the above equation as
\[ \Rightarrow {\rm{S}}{{\rm{T}}^2} = \left( {a{\rm{ }}\cos e{c^2}\dfrac{\alpha }{2}} \right)\left( {a{\rm{ }}\cos e{c^2}\dfrac{\beta }{2}} \right)\]
We know that \[{\rm{SP}} = a\cos e{c^2}\dfrac{\alpha }{2}\] and \[{\rm{SQ}} = a\cos e{c^2}\dfrac{\beta }{2}\]. Therefore we get
\[{\rm{S}}{{\rm{T}}^2} = {\rm{SP}} \cdot {\rm{SQ}}\]

Hence, we proved the equation.

Note:
We should know the different properties of the trigonometric function and the equation in polar form of a parabola. It is also important to remember in which quadrant the function is positive or negative. In the first quadrant all the functions i.e. sin, cos, tan, cot, sec, cosec are positive. In the second quadrant only sin and cosec function are positive and all the other functions are negative. In the third quadrant only tan and cot functions are positive and in the fourth quadrant only cos and sec function is positive.