Question

The tangent to the circle \[{C_1}:{x^2} + {y^2} - 2x - 1 = 0\] at the point\[\left( {2,1} \right)\] cuts off a chord of length 4 from a circle \[{C_2}\] whose center is \[\left( {3, - 2} \right)\]. The radius of \[{C_2}\] is
A. \[\sqrt 6 \]
B. 2
C. \[\sqrt 2 \]
D. 3

Answer 1

Hint: First we will first find the equation of tangent on \[{C_1}\] at \[\left( {2,1} \right)\] and when it cuts off the chord of the circle \[{C_2}\], then the obtained equation is the equation of the chord. Then we will use the distance of the chord of the circle to the point \[\left( {x,y} \right)\] is calculated using the formula, \[\dfrac{{\left| {ax + by + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\] and find the values of \[a\], \[b\], \[c\], \[x\], and \[y\] from comparing the obtained equation and above formula. Then we will substitute these values in the above formula of distance and use the Pythagorean theorem \[{h^2} = {a^2} + {b^2}\], where \[h\] is the hypotenuse, \[a\] is the height and \[b\] is the base of the right-angled triangle to find the required value.

Complete step by step answer:

We are given that the tangent to the circle \[{C_1}:{x^2} + {y^2} - 2x - 1 = 0\] at the point\[\left( {2,1} \right)\] cuts off a chord of length 4 from a circle \[{C_2}\] whose center is \[\left( {3, - 2} \right)\].

Finding the equation of tangent on \[{C_1}\] at \[\left( {2,1} \right)\], we get
\[
   \Rightarrow 2x + y - \left( {x + 2} \right) - 1 = 0 \\
   \Rightarrow 2x + y - x - 2 - 1 \\
   \Rightarrow x + y - 3 = 0 \\
 \]

Adding the above equation by 3 on both sides, we get
\[
   \Rightarrow x + y - 3 + 3 = 0 + 3 \\
   \Rightarrow x + y = 3{\text{ ......eq.(1)}} \\
 \]

If it cuts off the chord of the circle \[{C_2}\], then the above equation is the equation of the chord.

We know that the distance of the chord of the circle to the point \[\left( {x,y} \right)\] is calculated using the formula, \[\dfrac{{\left| {ax + by + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\].

Finding the values of \[a\], \[b\], \[c\], \[x\], and \[y\] from comparing the equations (1) and above formula, we get

\[a = 1\]
\[b = 1\]
\[c = - 3\]
\[x = 3\]
\[y = - 2\]

Substituting these values in the above formula of distance, we get
\[
   \Rightarrow \dfrac{{\left| {3\left( 1 \right) - 2\left( 1 \right) - 3} \right|}}{{\sqrt {{1^2} + {1^2}} }} \\
   \Rightarrow \dfrac{{\left| {3 - 2 - 3} \right|}}{{\sqrt {1 + 1} }} \\
   \Rightarrow \dfrac{{\left| { - 2} \right|}}{{\sqrt 2 }} \\
   \Rightarrow \dfrac{2}{{\sqrt 2 }} \\
   \Rightarrow \sqrt 2 \\
 \]

Thus, the distance is \[\sqrt 2 \].

We know that the length of the chord is 4.

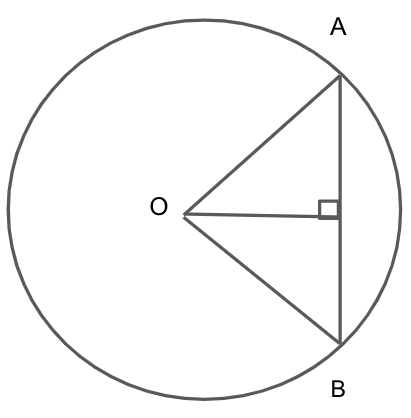
We will use the Pythagorean theorem \[{h^2} = {a^2} + {b^2}\], where \[h\] is the hypotenuse, \[a\] is the height and \[b\] is the base of the right angled triangle.

Applying the Pythagorean theorem in the triangle AOB, where OA is the radius of the triangle, we get

\[
   \Rightarrow O{A^2} = {2^2} + {\left( {\sqrt 2 } \right)^2} \\
   \Rightarrow O{A^2} = 4 + 2 \\
   \Rightarrow O{A^2} = 6 \\
 \]

Taking the square root on both sides in the above equation, we get

\[ \Rightarrow OA = \pm \sqrt 6 \]

Since the side can never be negative, the negative value of \[OA\] is discarded.
Thus, option A is correct.

Note: In solving these types of questions, students must know that while reading this problem one has to take care of all the steps to find the final answer. One should know the right time to use the Pythagorean theorem and the distance from the chord of the circle to the point.